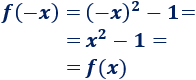Función simétrica
Una función f es simétrica con respecto al eje de ordenadas cuando para toda x del dominio se verifica: f(-x) = f(x).
Función simétrica
Cuando estudiamos la simetría de una función puede ocurrir que la función sea simétrica o no. En el caso de que la función sea simétrica hay dos tipos de simetría.
TIPOS DE SIMETRÍA
El carácter de las funciones puede ser de dos tipos:
- Simetría con respecto al eje OY, también llamada simetría uniforme: Diremos que una función tiene simetría para cuando la función f(x)=f(-x); ; es decir, cuando cada valor de la función en un punto, coincide con el valor de la función en el inverso. Por ejemplo, si f(5)=1, entonces f(-5)=1.
- De forma gráfica podemos realizarlo doblando la gráfica por el eje OY, de tal forma que la función sea asumida a ambos lados de la misma. Es decir, como si pusiéramos un espejo en ese eje.
- La simetría con respecto al origen, también llamada simetría impar: Diremos que una función tiene simetría impar cuando la función f(x)=-f(-x). Cuando una función tiene este tipo de simetría, significa que para cada valor de la función en un punto, es el valor opuesto del punto opuesto. Por ejemplo, si f(2)=6, entonces f(-2)=-6.
- De manera gráfica, podemos notar cuando si doblamos el papel por el eje OX, la función aparentemente tiene simetría con respecto al eje OY o incluso simetría; y si lo doblamos de nuevo por el eje OY, las funciones se superpondrán.
PASOS PARA DETERMINAR LA SIMETRÍA DE UNA FUNCIÓN
Para determinar analíticamente si una función es simétrica llevaremos a cabo dos pasos muy simples:
- Primero, encontraremos la función f(-x), para ello sustituiremos cada x por -x. Una vez hecho esto comprobaremos si f(x)=f(-x), si lo anterior es cierto diremos que la función es simétrica incluso o con respecto al eje OY, y terminaríamos los pasos. De lo contrario, pasaremos al siguiente paso.
- Una vez comprobado que el paso anterior no se cumple, encontramos -f(-x). Cambiaremos el signo de la función, teniendo en cuenta que en el caso de ser una función racional sólo cambiará el signo en el numerador o denominador. Si f(x)=-f(-x), diremos que la función tiene simetría impar o respecto al origen. En caso contrario, la función no tiene ningún tipo de simetría.
Ejemplo de Función simétrica
La siguiente función es par:
Demostración:
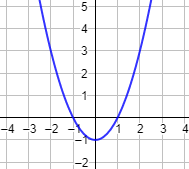
Gráfica:
Contenido