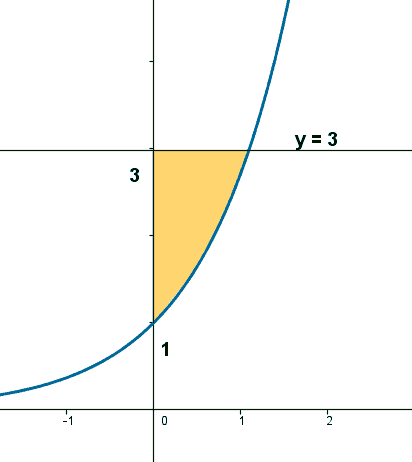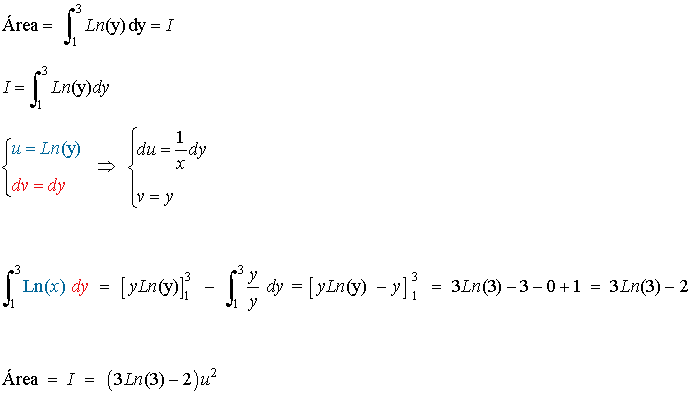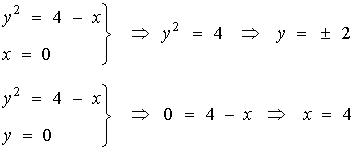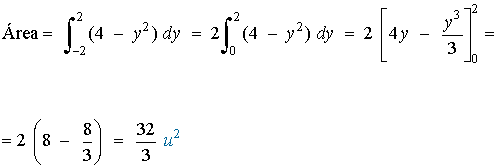Área entre las gráficas de funciones ejercicios resueltos
El área entre dos funciones es igual al área de la función arriba menos el área de la función abajo.
Área entre dos funciones
Para encontrar el área de la región limitada por dos funciones hacemos los siguientes pasos:
- Límites de la integración, para ello igualamos las funciones y resolvemos la ecuación resultante.
- Calculamos la función de diferencia de las dos funciones.
- Encontramos una primitiva de la función de diferencia G(x).
- En el área del recinto, sustituimos los valores de los límites de integración en la primitiva de la función de diferencia G(x) y los restamos.
Área entre las gráficas de funciones ejercicios resueltos
- Hallar el área de la región limitada por el eje de ordenadas, la recta y = 3 y la curva y = ex
Empezamos con la curva y = ex. Observamos primero que y' = ex, y'' = ex >0 y vemos que la función es convexa. Por otra parte si x = 0, entonces y = 1.
A la vista de la gráfica, es claro que tendremos que integrar sobre el eje de ordenadas entre 1 y 3. Por tanto, el área se calculará como de la siguiente forma:
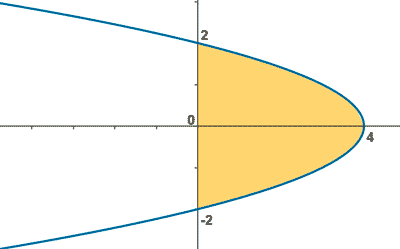
- Hallar el área limitada por la parábola y2 = 4 - x y el eje de ordenadas.
Puntos de corte
De manera que los puntos de corte son ( 0, 2 ) , ( 0, -2 ) con el eje de ordenadas y ( 4, 0 ) con el eje de abscisas.
En vista del gráfico del área, vemos que estamos interesados en integrar con respecto a y, por lo tanto:
Contenido
