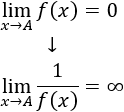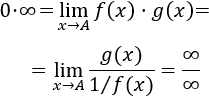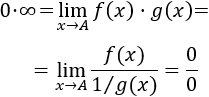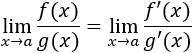
Cero por infinito
La mejor manera de evitar la indeterminación 0-∞ es transformarla en ∞/∞ o indeterminación 0/0.
Además, podemos aplicar L'Hôpital a estas indeterminaciones.
Supongamos que f(x) tiende a 0 y g(x)tiende a ∞. Entonces, la indeterminación 0-∞ aparece en el producto f(x)⋅g(x):
Dado que el límite de f(x) es 0, el límite de su inverso multiplicativo es ∞:
Por tanto, sólo tenemos que escribir el producto como un cociente:
Análogamente para :
Regla de L’Hôpital
La regla de L'Hôpital es el resultado del cálculo diferencial que permite calcular límites con la parte infinita indeterminada o la parte cero cero:
Si tenemos un límite con la indeterminación cero por infinito, podemos transformar la función para obtener una de las dos indeterminaciones que nos permite aplicar esta regla.
Supongamos que tenemos la indeterminación cero por infinito:
siendo 0 el límite de f(x) e infinito el límite de g(x).
Transformación a ∞/∞:
El límite del inverso de f(x) es infinito:
Por tanto,
Transformación a 0/0:
De forma similar,
Contenido