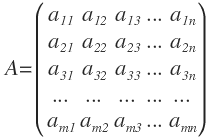
Matriz cuadrada
Una matriz cuadrada cumple con eso (m = n). En otras palabras, tiene el mismo número de filas y columnas. Por lo tanto, la dimensión de las filas será la misma que la de las columnas.
La matriz cuadrada es muy importante porque es la base de muchos tipos y métodos de matrices.
Matriz transpuesta
Una matriz transpuesta consiste en reordenar la matriz original cambiando las filas por columnas y las columnas por filas.
Por lo general, una matriz transpuesta se indica con un superíndice T o un apóstrofe ('). Para expresarlo mejor, optamos por el superíndice T.
Matriz de identidad
La matriz de identidad es una matriz cuadrada en la que todos sus elementos son ceros, excepto los pertenecientes a su diagonal principal. Generalmente se identifica con la letra I.
La matriz de identidad se puede distinguir rápidamente sin hacer ningún tipo de cálculo.
Matriz triangular
Una matriz triangular es una matriz cuadrada en la que los elementos que están debajo de la diagonal principal son ceros o los elementos que están encima de la diagonal principal son ceros.
La matriz triangular está centrada en la ubicación de los triángulos que contienen sólo ceros. Según su posición con respecto a la diagonal principal, la matriz de triángulos se denominará superior o inferior.
Matriz simétrica
Una matriz es simétrica si es una matriz cuadrada y coincide con su transposición (C=CT).
Para encontrar matrices simétricas de forma sencilla, sólo tenemos que mirar los triángulos de los elementos por encima y por debajo de la diagonal principal.
Contenido