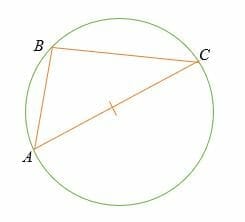
Thales theorem
El diámetro de un círculo siempre subtiende un ángulo recto a cualquier punto del círculo.
Notaste que el teorema de Tales es un caso especial del teorema del ángulo inscrito (el ángulo central = el doble del ángulo inscrito).
El teorema de Tales se atribuye a Tales, un matemático y filósofo griego que se basó en Mileto. Tales fue el primero en iniciar y formular el Estudio Teórico de la Geometría para hacer de la astronomía una ciencia más exacta.
Hay múltiples maneras de probar el Teorema de Tales. Tanto la geometría como las técnicas de álgebra pueden ser utilizadas para probar este teorema. Dado que este es un tema de geometría, por lo tanto, veamos el método más básico a continuación.
¿Cómo resolver el Teorema de Tales?
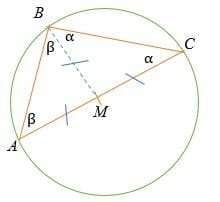
- Para probar el teorema de Tales, dibuja una bisectriz perpendicular de ∠
- Dejemos que el punto M sea el punto medio de la línea AC
- También deja que ∠MBA = ∠BAM = β y ∠MBC =∠BCM =α
- Línea AM = MB = MC = el radio del círculo.
- ΔAMB y ΔMCB son triángulos isósceles.
Por el teorema de la suma de los triángulos,
∠BAC +∠BAC +∠CBA = 180°
β + β + α + α = 180°
Factoriza la ecuación.
2 β + 2 α = 180°
2 (β + α) = 180°
Dividir ambos lados por 2.
β + α = 90°.
Por lo tanto, ∠ABC = 90°, por lo tanto se demuestra