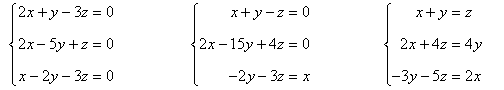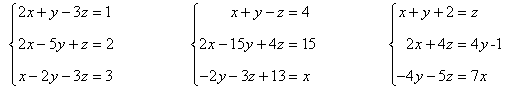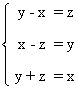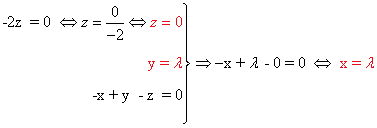Tipos de sistemas de ecuaciones lineales
- Un sistema de ecuaciones es homogéneo si todos sus términos independientes son cero.
- Un sistema de ecuaciones no homogéneo es aquel que tiene algunos de sus términos independientes no nulos.
Ejemplos de sistemas homogéneos y no homogéneos
Ejemplos de sistemas homogéneos
Ejemplos de sistemas no homogéneos
Ecuaciones lineales homogéneas
Los sistemas homogéneos son siempre compatibles (SCD o SCI), ya que la matriz de coeficientes y la matriz extendida tienen el mismo rango (al extender la matriz de coeficientes con un archivo de ceros el rango no varía).
Cuando un sistema homogéneo es Compatible Determinado (SCD), su única solución será la trivial: x=0 , y=0 , z=0
Definición de Ecuación diferencial homogénea
Observación: si la ecuación diferencial está escrita en la forma Una ecuación diferencial ordinaria de primer orden, , es homogénea si la función
es homogénea de orden cero.
sería homogénea sí y sólo sí los coeficientes y
son funciones homogéneos del mismo grado.
Sistemas homogéneos de ecuaciones lineales ejercicios resueltos
Resolver el siguiente sistema de ecuaciones
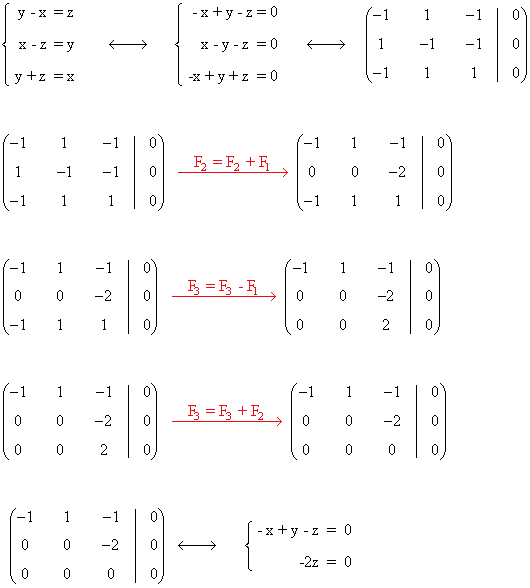
Empezamos aplicando Gauss:
Resolvemos el sistema equivalente:
Contenido