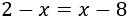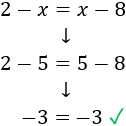
Ecuaciones de primer grado

Una ecuación de primer grado o una ecuación lineal es una igualdad algebraica cuya potencia equivale a uno, y puede contener una, dos o más incógnitas.

Ecuaciones de primer grado

Las ecuaciones de primer grado con un desconocido tienen la forma:

ax + b = c

Yendo a ≠ 0. Es decir, "a" no es cero. "b" y "c" son dos constantes. Es decir, dos números fijos. Finalmente, 'x' es la desconocida (el valor que no conocemos).

Elementos de una ecuación de primer grado

Observando la siguiente ilustración, nos daremos cuenta de que varios elementos están involucrados en una ecuación. Veamos:

Como se puede ver en el gráfico anterior, una ecuación tiene varios elementos:

Términos
Miembros
Incógnita
Términos separados

Resolver las ecuaciones de primer grado con una incognita

Prácticamente, resolver una ecuación, en este caso, de primer grado es determinar el valor de lo desconocido que satisface la igualdad. Los pasos son los siguientes:

Agrupar los términos similares. Es decir, proceder a pasar los términos que contienen variables al lado izquierdo de la expresión y las constantes al lado derecho de la expresión.
Finalmente, proceder a limpiar lo desconocido.

Ejemplo de ecuaciones de primer grado

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$
Solución

Para resolver la ecuación, debemos pasar los monomios que tienen lo desconocido en un lado de la igualdad y los que no tienen lo desconocido en el otro lado.

Como 8 es la resta a la derecha, pasa la suma al lado izquierdo:

Como x está restando a la izquierda, pasa restando a la derecha:

Ahora que hemos separado los monomios con y sin lo desconocido, podemos sumarlos. A la izquierda, añadimos
2+8 y, a la derecha, x+x:

Entrada Relacionada: Combinaciones sin repetición

Para ver claramente el siguiente paso, escribimos 2x como producto:

Para terminar, debemos pasar el coeficiente de lo desconocido (el número 2 que multiplica a x) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:

Simplificando la fracción,

Por lo tanto, la solución de la ecuación es x=5. Para comprobar la solución, sustituimos x por 5 en la ecuación:

Como hemos obtenido una verdadera igualdad (-3 es igual a -3), la solución es correcta. Si, por el contrario, obtenemos una falsa igualdad, significa que hemos cometido algún error en la solución de la ecuación.

Contenido