¿Qué es un vector?
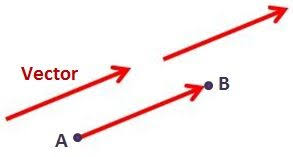
Un vector es un segmento de línea en el espacio que comienza de un punto a otro, es decir, tiene dirección y sentido. Los vectores en la física tienen la función de expresar las llamadas magnitudes vectoriales.
Componentes de un Vector
Los componentes de los vectores que definen sus características son los siguientes:
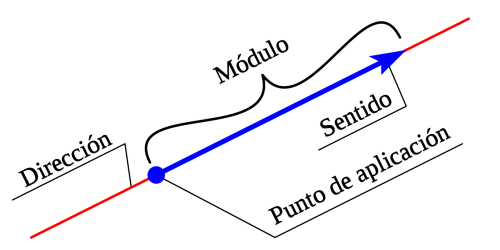
Módulo o magnitud: se refiere a la longitud o amplitud del segmento de vector o línea.
Dirección: se refiere a la inclinación del vector con respecto a un eje horizontal imaginario, con el que forma un ángulo.
Dirección: se refiere a la orientación del vector, indicada por la cabeza de la flecha del vector.
Tipos de vectores
- Vectores nulos: son aquellos en los que el origen y el final coinciden y, por lo tanto, el módulo o la magnitud es igual a 0.
- Vectores unitarios: son aquellos cuyo módulo es igual a 1.
- Vectores fijos: son aquellos que expresan un punto de origen así como un punto final, que se determina en un punto fijo del espacio. Suelen utilizarse, por ejemplo, para expresar la fuerza aplicada a ese punto. Para representarlos, se dice que el punto de origen es A y el final es B.
- Vectores paralelos: están situados en líneas paralelas, pero tienen la misma dirección o la opuesta.
- Vectores opuestos: se caracterizan por tener la misma dirección y magnitud, pero su sentido es opuesto.
- Vectores concurrentes o angulares: son aquellos cuyas líneas de acción pasan por el mismo punto, es decir, se intersectan.
- Vectores libres: son aquellos vectores cuyo punto de aplicación es indeterminado y por lo tanto libre.
- Vectores equipolentes o iguales: son aquellos vectores con el mismo módulo, dirección y sentido.
- Vectores coplanares: son aquellos vectores que están en el mismo plano.
- Vectores colineales: son aquellos vectores cuyas líneas de acción están en la misma línea.
- Vectores axiales o pseudo-vectores: son los que están ligados a efectos de rotación. La dirección indica el eje de rotación del segmento.
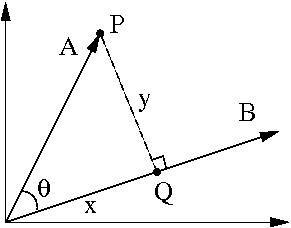
Proyección de vectores
Hay dos tipos de proyecciones vectoriales:
Proyección U-in-V y proyección V-in-U. Las explicaremos una por una.
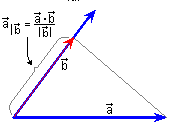
Proyección de U en V
La proyección de U en V es proporcional a V
La forma de calcularlo es la siguiente:
Proyecto v U = [(U.V)/|V|^2] V
Donde U.V. es el punto producto de los vectores, |V|^2 es la magnitud del vector V al cuadrado y toda esa operación por V que es el vector.
Proyección de V en U
La proyección de V en U es proporcional a U.
La forma de calcularlo es la siguiente:
Proyección V = [(U.V)/|U|^2] U
Donde U.V. es el punto de producto, |U|^2 es la magnitud de U al cuadrado y toda esa operación se multiplica por U.
Contenido