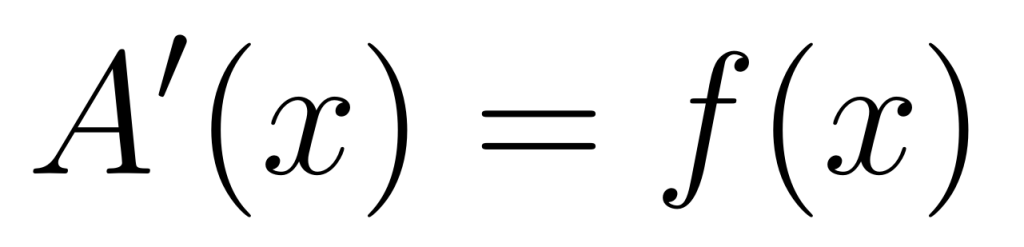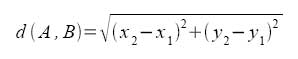Propiedades de la integral indefinida
La integral indefinida de la suma algebraica de dos o más funciones es igual a la suma de sus integrales.
Propiedades de la integral indefinida
Sea definimos una anti-derivación (primitiva en algunos libros de texto) de la misma como una función
tal que al derivarla, obtenemos la función
, es decir, un función que cumple con la siguiente condición:
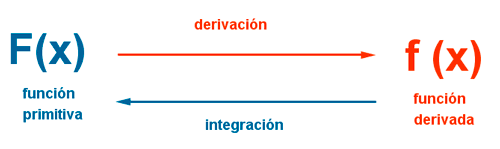
- La integración es la función inversa de la derivación
- La integral indefinida nos permite encontrar una función conocida como su derivada.
La integral definida es la que nos permite calcular el área de las figuras planas delimitadas por curvas o volúmenes de revolución.
Primitiva o antiderivada de una función
F(x) es una primitiva de f(x) cuando la derivada de F(x) sea f(x)
F(x) es una primitiva de f(x) ⇔ F ' (x) = f(x)
Ejemplos de primitivas de una función
- Una primitiva de cos x es sen x ya que (sen x)' = cos x
- Una primitiva de 2x es x2 puesto que (x2)' = 2x
- Una primitiva de ex es ex ya que (ex)' = ex
Propiedades de integral indefinida
Tabla de Integrales

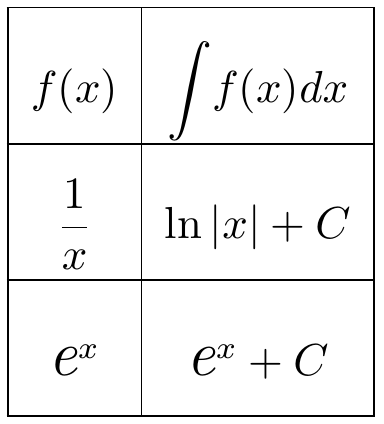
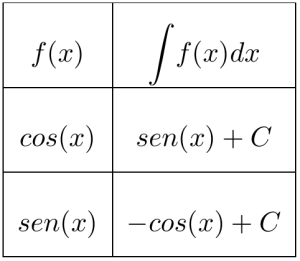
Contenido