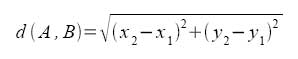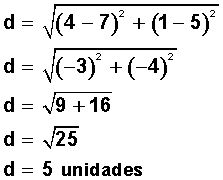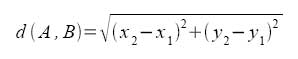
Distancia entre dos puntos 
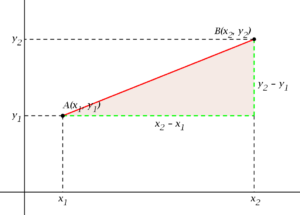
Dados dos puntos cualesquiera A(x1,y1), B(x2,y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento que los separa.
Para calcularla aplicamos el teorema de Pitágoras en el rectángulo coloreado :
Si los puntos tienen la misma ordenada o el mismo abismo, la distancia entre ellos se calcula sin aplicar la fórmula anterior.
Distancia entre dos puntos en el plano cartesiano
El Plano Cartesiano se utiliza como sistema de referencia para localizar puntos en un plano.
Otra utilidad de dominar los conceptos sobre el Plano Cartesiano es que, a partir de la ubicación de las coordenadas de dos puntos, es posible calcular la distancia entre ellos.
- Cuando los puntos se encuentran en el eje x (de las abscisas) o en una línea paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 - x1).
- Cuando los puntos están situados en el eje y (de las ordenadas) o en una línea paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 - y2)
Distancia entre dos puntos ejercicios
Ejemplo:
La distancia entre los puntos (-4, 0) y (5, 0) es de 5 - (-4) = 5 +4 = 9 unidades.
Cuando los puntos están situados en el eje y (de las ordenadas) o en una línea paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora bien, si los puntos están situados en cualquier lugar del sistema de coordenadas, la distancia viene determinada por la relación:
Contenido