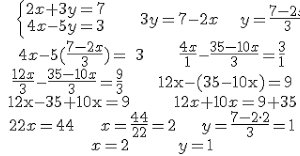Probabilidad de eventos independientes
Esta circunstancia se produce siempre que el proceso que genera el resultado del evento 1 no altere en modo alguno la probabilidad de los posibles resultados del evento 2.
Una situación de eventos independientes es la siguiente: supongamos que se lanzan dos dados de seis caras, uno azul y otro rosa. La probabilidad de que se tire un 1 en el dado azul es independiente de la probabilidad de que se tire -o no- un 1 en el dado rosa.
Otro caso de dos eventos independientes es el lanzamiento de la moneda. El resultado de la primera tirada no dependerá del resultado de la segunda y viceversa.
Demostración de dos eventos independientes
Para verificar que dos eventos son independientes, pasaremos a definir el concepto de probabilidad condicionada de un evento con respecto a otro. Para ello es necesario diferenciar entre los eventos excluyentes y los eventos incluyentes:
Dos sucesos son exclusivos si los posibles valores o elementos del suceso A, no tienen nada en común con los valores o elementos del suceso B.
Por lo tanto, en dos eventos excluyentes, el conjunto de la intersección de A con B es el vacío:
Eventos excluyentes: A∩B = Ø
A la inversa, si los acontecimientos son inclusivos, puede ser que un resultado del acontecimiento A coincida también con el de otro B, siendo A y B acontecimientos diferentes. En este caso:
Eventos inclusivos: A∩B ≠ Ø
Esto nos lleva a definir la probabilidad condicionada de dos eventos inclusivos, es decir, la probabilidad de que ocurra el evento A, siempre que ocurra el evento B:
P(A∩B) = P(A∩B)/P(B)
Por lo tanto, la probabilidad condicionada es la probabilidad de que A y B ocurran dividida por la probabilidad de que B ocurra. También puede definirse la probabilidad de que B ocurra condicionalmente a A:
P(A∩B) = P(A∩B)/P(A)
Criterios para saber si dos eventos son independientes
A continuación daremos tres criterios para saber si dos eventos son independientes. Basta con que se cumpla uno de los tres para que se demuestre la independencia de los acontecimientos.
Si la probabilidad de que A ocurra cuando ocurre B es igual a la probabilidad de A, entonces son eventos independientes:
P(A¦B) = P(A) => A es independiente de B
Si la probabilidad de que B ocurra dada A, es igual a la probabilidad de B, entonces tienes eventos independientes:
P(B¦A) = P(B) => B es independiente de A
Si la probabilidad de que A y B ocurran es igual al producto de la probabilidad de que A ocurra por la probabilidad de que B ocurra, entonces son eventos independientes. Lo recíproco también es cierto.
P(A∩B) = P(A) P(B) <=> A y B son eventos independientes.
Probabilidad de eventos independientes ejercicios resueltos
Se comparan las suelas de goma producidas por dos proveedores diferentes. Las muestras de cada fabricante se someten a varias pruebas de las que se concluye si están o no dentro de las especificaciones.
El resumen resultante de las 252 muestras es el siguiente:
Fabricante 1; 160 cumplen las especificaciones; 8 no cumplen las especificaciones.
Fabricante 2; 80 cumplen las especificaciones; 4 no cumplen las especificaciones
Evento A: "que la muestra es del fabricante 1".
Evento B: "que la muestra cumple con las especificaciones".
Deseamos saber si estos eventos A y B son independientes o no, para lo cual aplicamos uno de los tres criterios mencionados en la sección anterior.
Criterio :
P(B¦A) = P(B) => B es independiente de A
P(B) = 240/252 = 0,9523
P(⋂) = P(A ⋂ B)/P(A) = (160/252) / (168/252) = 0,9523
Conclusión: Los eventos A y B son independientes.
Supongamos el evento C: "que la muestra proviene del fabricante 2"
¿Será el evento B separado del evento C?
Aplicamos uno de los criterios.
Criterio : P(B¦C) = P(B) => B es independiente de C
P(B¦C) = (80/252) / (84/252) = 0.9523 = P(B)
Por lo tanto, según los datos disponibles, la probabilidad de que una suela de goma seleccionada al azar cumpla las especificaciones es independiente del fabricante.
Contenido