Máximos y mínimos de una función de dos variables ejercicios resueltos
Los siguientes problemas resueltos son problemas de optimización utilizando el cálculo diferencial básico (nivel de secundaria). Para resolverlos, es necesario derivar y aplicar el criterio de la primera derivada.
Máximos y mínimos de una función de dos variables ejercicios resueltos
- Un triángulo isósceles de perímetro 30 cm, gira alrededor de su altura
engendrando un cono.
¿Qué valor debe darse a la base para que el volumen del cono sea máximo?

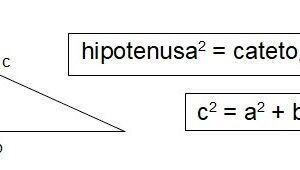
Función a optimizar:
![]()
Relacionamos las variables:
![]()
![]()
![]()
Sustituimos en la función:
![]()
Derivamos, igualamos a cero y calculamos las raíces.

![]()
![]()
Realizamos la derivada segunda para comprobar el resultado obtenido


![]()
Así, el criterio de la segunda derivada establece que "si la segunda derivada es inferior a cero (negativa), entonces la función tiene un máximo relativo. En conclusión, para el radio máximo de 6, hay un máximo relativo