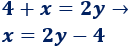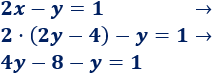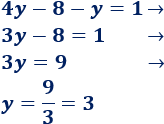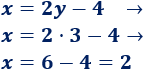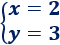¿Cómo se clasifica un sistema de ecuaciones?
Los sistemas de ecuaciones lineales pueden clasificarse según su número de soluciones:
- Compatible determinado: Tiene una sola solución, la representación son dos líneas que se cortan en un punto.
- Indeterminado compatible: Tiene infinitas soluciones, la representación son dos rectas que coinciden.
- Incompatible: No tiene solución, la representación son dos líneas paralelas.
Método de Sustitución paso a paso
Para resolver un sistema de ecuaciones por el método de sustitución seguiremos los siguientes pasos:
- Una incógnita se borra en una de las ecuaciones
- La expresión de esta desconocida se sustituye en la otra ecuación, obteniendo una ecuación con una sola desconocida
- La ecuación está resuelta
- El valor obtenido se sustituye en la ecuación donde las incógnitas eran claras
- Los dos valores obtenidos constituyen la solución del sistema
Ejercicios resueltos de sistemas de ecuaciones por el método de sustitución
Aislamos la incógnita
Aislemos la x de la primera ecuación. Como su coeficiente es 1, sólo tenemos que pasar el 4 restándolo del otro lado:
Ya hemos aislado la x
Sustituimos la incógnita en la otra ecuación
Como tenemos que x es igual a 2y-4, escribimos 2y-4 en lugar de x en la segunda ecuación (sustituimos la x):
Resolvemos la ecuación obtenida
Ya sabemos que y=3.
Calculamos la otra variable sustituyendo
Al borrar la x tuvimos
Como sabemos y=3, sustituimos en la ecuación:
Por lo tanto, la otra incógnita es x=2.
La solución del sistema es
Contenido