Ecuaciones cuadráticas o de segundo grado
Las ecuaciones cuadráticas o de segundo grado son aquellas en las que el exponente del término desconocido se eleva al cuadrado, es decir, lo desconocido se eleva al exponente 2:
donde a, b y c son números reales y se conocen como coeficientes. Así, a es el coeficiente de x2, b es el término o coeficiente de x y c es el término independiente.
Si a = 1, la ecuación cuadrática es reducida. Si a = 0, entonces deja de ser una ecuación de segundo grado, y se transforma en una ecuación de primer grado:
Cómo resolver ecuaciones cuadráticas paso a paso
Para resolver una ecuación de segundo grado usando la fórmula general:
- Identificamos los coeficientes a, b y c.
- Los sustituimos en la fórmula general.
- Calculamos x1 sumando el discriminante y x2 restando el discriminante.
Debemos tener en cuenta que:
solo hay una raíz para la ecuación.
hay dos raíces con números reales.
no hay una solución real.
Ejemplos gráficos de ecuación de segundo grado
Una ecuación de segundo grado corresponde a una parábola que abre hacia arriba o hacia abajo.
Una función cuadrática se define como f(x)=ax^2+bx+c, para todos los a, b y c que pertenecen a los números reales, debe ser diferente de cero.
- Si a>0, la parábola abre hacia arriba y su vértice es el valor mínimo de la función, es decir, el punto más bajo de la parábola.
- Si a>0, la parábola abre hacia abajo y su vértice es el valor máximo de la función, es decir, el punto más alto de la parábola.
Además, estas funciones cuadráticas presentan simetría respecto a un eje de simetría que pasa por el vértice de la parábola, el lado derecho de la curva es idéntico al lado izquierdo de la misma.
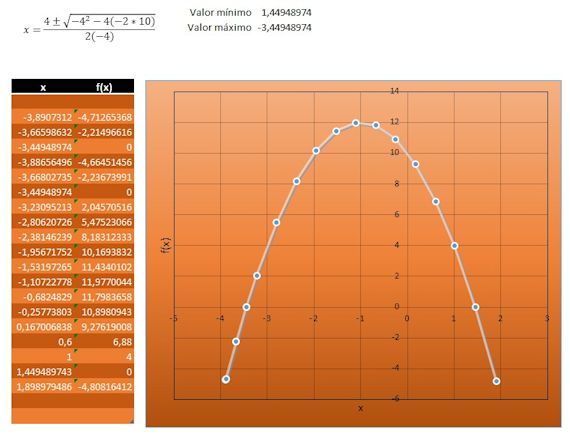
Ejemplo de representación de una función cuadrática
Calcular la función, la tabla y el gráfico para la ecuación –2x2 + 6 = 4x –4
Comenzamos por hacer que el resultado de la ecuación sea igual a cero:
Restamos 4 en ambos lados: (–2x2 + 6) – (4x–4) = (4x–4) – (4x–4)
Obtenemos –2x2 – 4x +10 = 0
Contenido