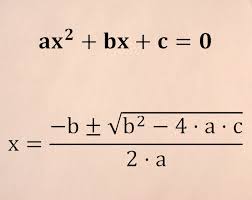
Integral definida
Con la idea de conocer un poco más a fondo este término que ahora se conoce, es importante comenzar desde el momento en que se creó el cálculo integral a mediados del siglo XVII y, después de su desarrollo que fue intuitivo y llevó un par de siglos, todo el concepto de lo que es la noción de integración comenzó a analizarse con el máximo rigor, esto a mediados del siglo XIX. A partir de ahí empezamos a conocer cuál fue la primera noción de integración según el concepto de Reimann integral o, como se conoce su generalización, Reimann-Stineltjes integral.
Cuando comenzó el siglo XX todo lo que es la teoría de la medida vivió un desarrollo tan grande que elevó el concepto a uno más general y mucho más avanzado que es el integral de Lebesgue. Con el paso del tiempo se desarrolló más la noción de proceso estocástico que estaba dentro de lo que era la teoría de la probabilidad y que llevó a la formulación de la integral de Itō cuando se vivía la mitad del siglo XX y después de eso se generalizó y se conoció en todas partes como la integral de Skorohod.
Las propiedades de la integral definida
En todo el proceso de la integral definida, se deben incluir las siguientes propiedades:
- El resultado final es igual a cero en toda la integral extendida a un intervalo que contiene un solo punto, [a, a].
- En el caso de que una función f (x) sea mayor que cero, su integral debe ser positiva. En cambio, si la función es menor que cero, su integral debe ser negativa.
- Para determinar la integral de una suma de funciones, sus integrales deben ser sumadas, pero cada una por separado.
- Esta propiedad establece que la integral del producto de una constante multiplicada por una fracción, el resultado debe ser el mismo que se obtiene al multiplicar la constante por la integral de la fracción. Entendemos entonces que la constante puede ser extraída de la misma integral.
- Hay un cambio de signos en la integral cuando sus límites son permutables.
- Cuando hay tres puntos en los que a < b < c, debe completarse con lo que se conoce como la integración de la fracción
Integral definida ejercicios resueltos
Utilizamos las fórmulas definidas para integrar :
Ahora , lo siguiente es evaluar esa función en los puntos 0 y 2:
Ahora, en el extremo superior, restamos el del extremo inferior del intervalo:
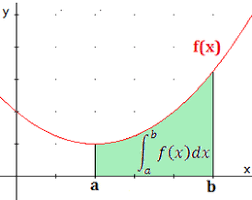
La integral definida en ese intervalo es 6. Eso significa que el área bajo la curva de esa ecuación en ese mismo intervalo es de 6 unidades.
Contenido