Conceptos previos de las leyes de Kirchhoff
Un circuito electrónico es la interconexión de componentes por:
- Nodos: definidos como el punto de conexión de dos o más componentes.
- mallas: que se define como un camino cerrado que incluye dos o más nodos.
- Dado un circuito (nodos y mallas) los voltajes y corrientes cumplen con las leyes de Kirchhoff.
Primera ley de Kirchhoff. Ley de las corrientes de Kirchhoff
Esta ley axiomática se llama Ley de Corrientes de Kirchhoff (abreviada LCK), que simplemente establece que
La suma algebraica de las corrientes que entran en cualquier nodo es igual a cero.
Esta ley representa una declaración matemática del hecho de que la carga no se acumula en un nodo. Por consiguiente, las corrientes deben sumar a cero.
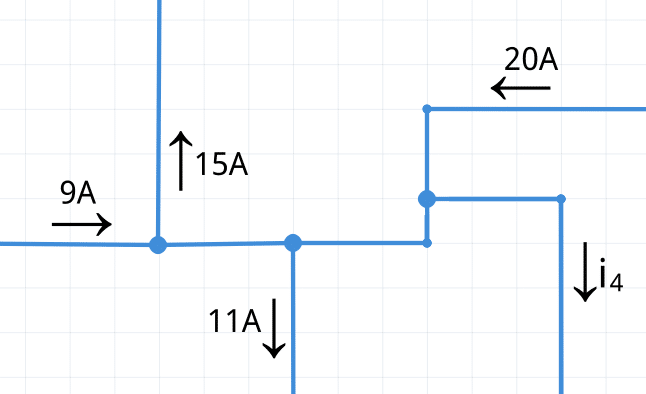
La siguiente ilustración se utilizará para la aplicación de la LCK:
Muestra las direcciones del flujo de corriente en un nodo.
¿Cuál es la corriente de i4 en el nodo distribuido?
Esta pregunta pone a prueba sus habilidades con flechas y signos. Las direcciones de las flechas están mezcladas, algunas entran y otras salen del nodo.
Se recomienda que redibuje el nodo con todas las flechas apuntando en la misma dirección. En este caso todas se dibujan hacia afuera.
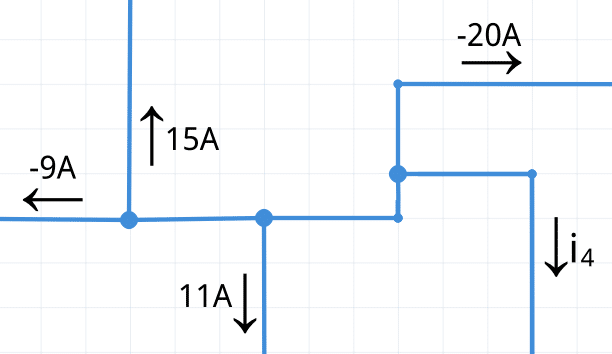
Si cambias la dirección de una flecha, también debes cambiar su signo.
Una vez que cambie la dirección de la corriente y haga los ajustes necesarios en los signos numéricos, tendrá lo siguiente:
Aplicando la ley actual de Kirchhoff y borrando la corriente i4, se obtiene el valor final de la corriente.
−9A+15A+11A+i4−20A=0
i4=+9A-15A-11A+20A
i4=3A
Segunda ley de Kirchhoff. Ley de las tensiones de Kirchhoff
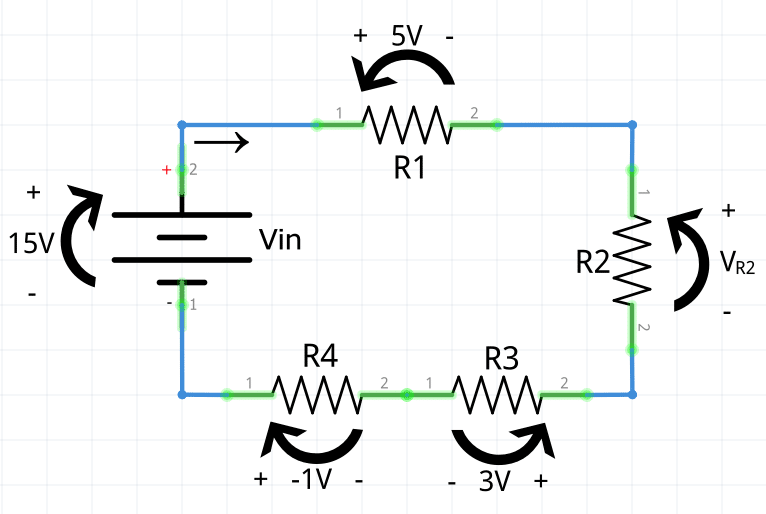
Con la ayuda de la Ley de Voltaje de Kirchhoff, encuentra el voltaje de la resistencia R2.
Primero elige un nodo para iniciar el análisis. En este ejemplo comenzó con el nodo que conecta R4 a la fuente de voltaje. Ahora sigue el camino en el sentido de las agujas del reloj alrededor del camino.
Las flechas de voltaje están mezcladas, no todas apuntan en la misma dirección alrededor del camino. Por lo tanto, presta mucha atención a la polaridad del voltaje de cada elemento del bucle. Dependiendo de la dirección de la flecha de voltaje, se define el signo más o menos.
Conseguir los signos correctos para la ecuación es la parte difícil. Esta es la habilidad esencial al aplicar las leyes de Kirchhoff. Con la ayuda del LVK se obtiene la siguiente ecuación:
15V+(−5V)+(−V R2)+(−3V)+(−1V)=0
15V−5V−VR2−3V−1V=0
6V−VR2=0
VR2=6V
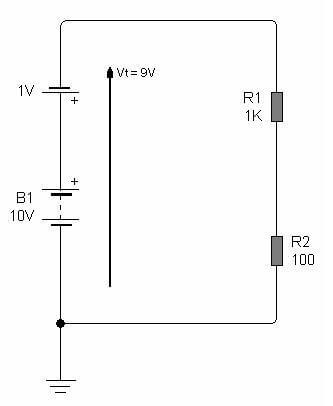
Procedimiento para resolver circuitos con las leyes de Kirchhoff
Observando las cuatro flechas de los voltajes de la fuente y las caídas de voltaje, se puede verificar el cumplimiento de la segunda ley de Kirchhoff. Ya que partiendo de la masa de referencia y girando en el sentido de las agujas del reloj podemos decir que
10V - 8,17V - 1V - 0,817 = 0V
O bien, haciendo una transposición de términos y dejando las fuentes a la derecha y las caídas de tensión a la izquierda podemos decir que la suma de las caídas de tensión de las fuentes 10V - 1V es igual a la suma de las caídas de tensión o diferencias de potencial 8,17V + 0,817 = 8,987 aproximadamente 9V.
Y también podemos calcular fácilmente que el voltaje en la salida del circuito es 0,817V + 1V = 1,817V con la polaridad indicada en el circuito, es decir, positiva.
Contenido