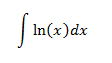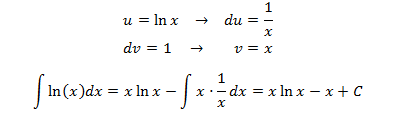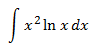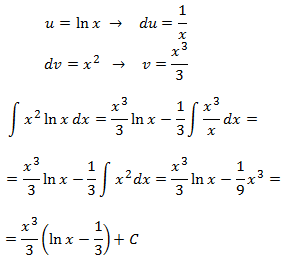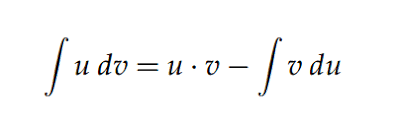
Integración por partes
Este método se basa en la aplicación de la siguiente fórmula:
donde:
u es una función y du es su derivada
v es una función y dv es su derivada
El método se aplica, sobre todo, cuando el integrando es un producto de función.
El método de integración por partes se basa en el derivado de un producto de función como se muestra a continuación
d(u-v) = u dv + v du
Por eso se usa para integrales que contienen dos funciones que se multiplican juntas.
∫d(u-v) = ∫u dv + ∫v du
Se llama integración por partes porque la integral se divide en dos partes: en una la integral es u y en la otra es v. La integral debe ser completa y sin alterar la operación dentro de ella. Consejo:
- La función correspondiente a dv debe ser la función más fácil de integrar
- En u deben ir aquellas funciones que no tienen integral directa (funciones logarítmicas e inversas), entonces las funciones algebraicas pueden ser consideradas ya que la derivada es reductora. Las funciones trigonométricas y exponenciales son más fáciles de trabajar.
Ejercicios resueltos
En esta integral no tenemos un producto explícito de funciones, pero como no sabemos cuál es el primitivo del logaritmo, lo que hacemos es derivarlo, es decir, u = ln (x).
Nos interesa elegir u = x2 (para reducir su exponente) pero entonces nos vemos obligados a obtener dv = ln(x) y obtener v no es inmediato. Así que elegimos lo contrario:
Contenido