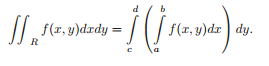
Integrales iteradas

La expresión de la derecha representa el proceso que comienza integrando la función f con respecto a z, tomando x e y como constantes, lo que resulta en una función de dos variables. La integración iterada de esa función, primero con respecto a y y luego con respecto a de, da como resultado el valor de la triple integral.

Integrales iteradas

En los artículos anteriores hemos visto diferentes métodos para resolver integrales, así como sus aplicaciones, pero siempre con funciones definidas en una variable. Ha llegado el momento de estudiar las integrales definidas de funciones de dos variables f(x,y) con respecto a estas dos variables en una cámara cerrada R. Por lo tanto, hoy vamos a extender el concepto que teníamos de integral definida de una función en un intervalo cerrado [a,b] a la doble integral definida en la cámara cerrada R=[a,b]x[c,d].

Sea f(x,y) una función continua para los valores de x,y que pertenecen a R. Para una y fija obtenemos la función F(x)=f(x,y) que también es continua y por lo tanto integrable en [a,b].

La función obtenida, G(y), es continua y por lo tanto integrable en [c,d] de tal forma que podemos definir la doble integral de la función f(x,y) el rectángulo R=[a,b]x[c,d] como:

Es decir, realizar una doble integral consiste en realizar dos integrales simultáneas, una en primer lugar en función de x, considerando que y es una constante; y en segundo lugar en función de y (en este caso ya no habrá término con x).

El valor que obtenemos al resolver la integral es un número real que se utiliza para determinar el valor del volumen del sólido situado verticalmente en el rectángulo R del plano OXY bajo la superficie z=f(x,y) siempre que f(x,y)≥0.

Entrada Relacionada: Common denominator

PROPIEDADES

La propiedad de la linealidad se cumple
Si hay un escalar multiplicador dentro de la integral se puede obtener un factor común.
La integral de la suma de dos funciones dobles f(x,y) + g(x,y) es igual a la suma de la integral doble de cada una de ellas:
Cumplen con la propiedad de la monotonía.
Si f(x,y)≤g(x,y) para todos los valores de (x,y) pertenecientes a R, entonces ∫∫f(x,y)dxdy ≤ ∫∫g(x,y)dxdy.
Si el recinto R puede dividirse en dos recintos separados R1 y R2, es decir, de tal manera que R1 U R2 = R y cuya intersección está vacía o lo que es lo mismo que R1∩R2 no tiene área.
La función del valor absoluto, |f(x,y)| también es integrable.

Recordemos que también podemos hacer integrales dobles en recintos que no son rectángulos, estas integrales se estudian más a fondo en carreras de ciencias como la ingeniería, así que por ahora, este ha sido un buen comienzo.