Regla de tres inversa
Las reglas de tres nos permiten despejar las incógnitas a valores que no conocemos. Por lo tanto, le mostramos cómo hacer una regla compuesta de tres, directa e inversa.
La regla de tres es una operación matemática que utilizamos para resolver eficaz y rápidamente los problemas de proporcionalidad. Estos problemas pueden plantearse de tal manera que la operación a realizar que se nos propone es una regla directa simple de tres, una regla inversa de tres, una regla compuesta de tres o una regla de tres por ciento.
Regla de tres directa
Siempre necesitamos 3 datos básicos: dos magnitudes que serán proporcionales entre sí, y una tercera magnitud. Lo que debemos averiguar es un cuarto término, que estará dentro de esta proporcionalidad. Tenemos 3 datos conocidos, que llamaremos a, b y c, y el cuarto dato desconocido, que será el desconocido a ser aclarado, por lo tanto: x.
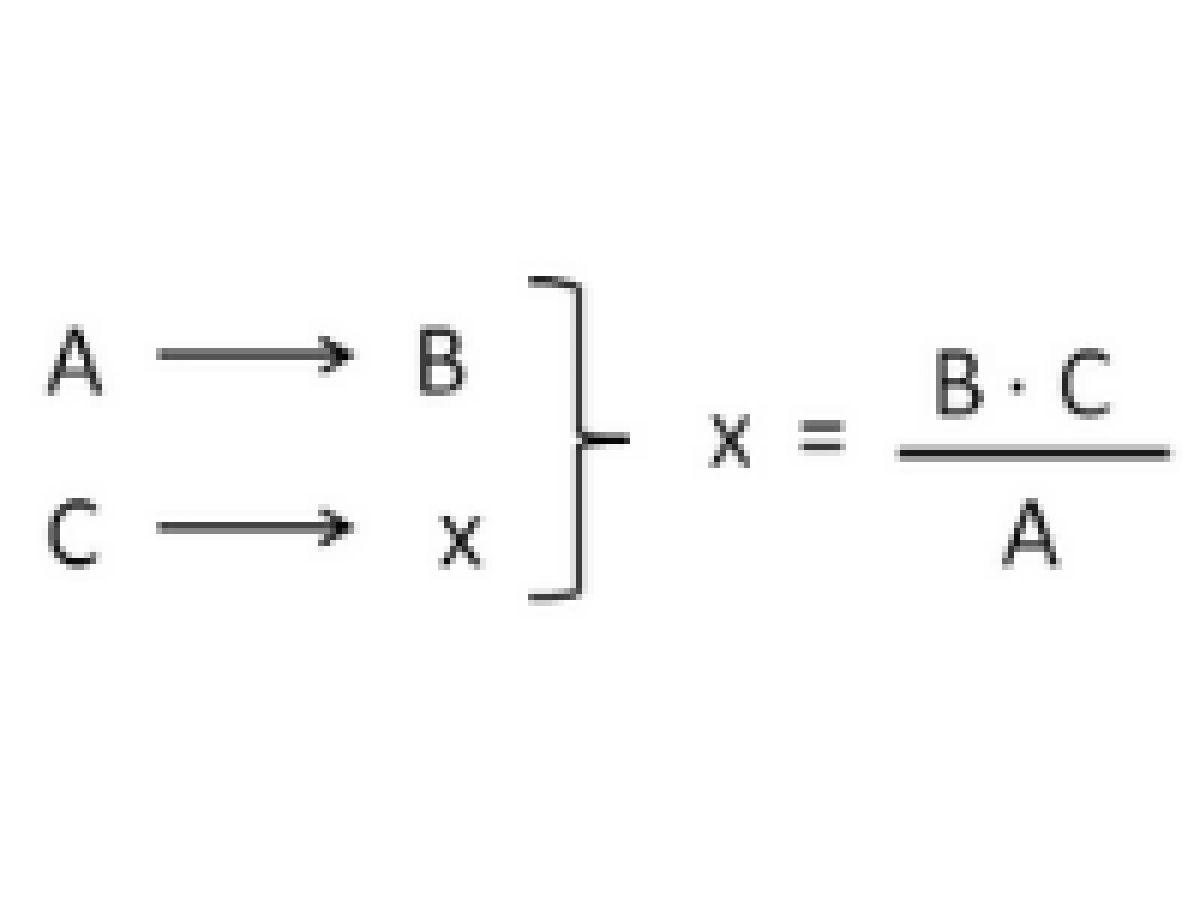
La fórmula que se aplicará será la siguiente:
Vemos, pues, que el resultado de multiplicar "b" x "c" y dividirlo por "a" será el valor de la desconocida x.
Regla de 3 inversa simple
En este tipo de operación, cuando una magnitud aumenta, otra disminuye, se llama por lo tanto la regla de tres inversa. En este caso, el resultado de multiplicar "a" x "b" y dividirlo por "c" será el valor de la x desconocida.
Regla de tres compuesta
Su uso se hace cuando se relacionan tres o más magnitudes, de modo que de las relaciones que se establezcan entre las magnitudes que ya conocemos, obtendremos lo desconocido.
Regla de tres simple inversa ejemplo
En este caso tenemos que:
En la regla de los tres inversos simples, en la relación entre los valores, se cumple que
y decimos que A es a B inversamente proporcional, como C es a D.
Conociendo los valores A, B y C, el valor D será:
Por ejemplo: "Un grifo con un flujo de 18 litros por minuto tarda 14 horas en llenar un tanque. ¿Cuánto tiempo tardaría si su flujo fuera de 7 litros por minuto?
La relación de proporcionalidad es inversa, ya que cuanto más flujo de agua tiene el grifo, menos tiempo (en horas) tarda en llenar el tanque. Así es:
Con un grifo de 7 litros por minuto de flujo (menos flujo) necesitamos 36 horas (más tiempo) para llenar el tanque.
Contenido
