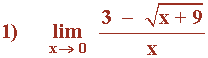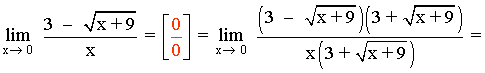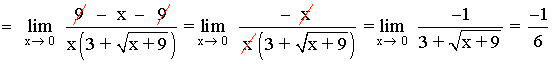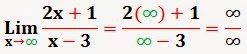L'Hôpital
L'Hôpital, antes de convertirse en el matemático que llegó a ser, comenzó una carrera fallida como militar. Además de ser conocido por la regla de L'Hôpital, también es conocido por haber resuelto el problema del braquicocráneo (la curva entre dos puntos para que se pueda recorrer en menos tiempo).
Es también el autor del primer libro conocido sobre cálculo diferencial en el que también incluye algunas de las explicaciones o clases de su profesor Johann Bernoulli. Por lo tanto, la regla de L'Hôpital es también conocida como la regla de L'Hôpital-Bernoulli.
El principal uso de la regla L'Hôpital es la resolución de los límites de indeterminación 0/0 o la de ∞/∞, mediante el uso de derivados.
Declaración: Sean f(x) y g(x) dos funciones continuas y derivables en un intervalo (a, b) que contenga el punto xo, de manera que:
- El límite de la función f(x) en el punto xo, así como el de g(x), es 0
- La derivada de la función g(x) es distinta de cero en cualquier punto del intervalo x que sea diferente de xo: g'(x)≠0.
- Existe el límite del cociente de las respectivas derivadas en el punto xo
Límite tiende a cero
- La regla de L'Hôpital puede aplicarse tantas veces como sea necesario siempre que se sigan cumpliendo las condiciones de la declaración, hasta que se encuentre el valor del límite.
- Esta regla también puede aplicarse a otros tipos de indeterminación, siempre que hayamos realizado las transformaciones necesarias para convertir la indeterminación en una del tipo necesario para aplicar L'Hôpital: 0/0 o la de ∞/∞.
Ejemplo de límite tiende a cero
Hallar los siguientes límites:
Multiplicamos y dividimos por el conjugado de la función:
Contenido