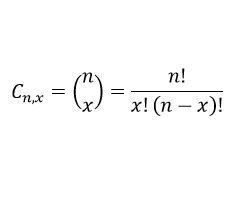
Combinaciones sin repetición
La combinatoria sin repetición se utiliza comúnmente en estadística y matemáticas. Se ajusta a muchas situaciones de la vida real y su aplicación es bastante simple.
Pensemos por ejemplo en un estudiante que tiene un examen de 4 preguntas. De las 4 preguntas tiene que elegir tres. ¿Cuántas combinaciones diferentes podría hacer el estudiante? Si razonáramos un poco veríamos (sin aplicar la fórmula) que el estudiante podría elegir cómo responder a las 3 preguntas de cuatro maneras diferentes.
- Conjunto/opción 1: Responder a las preguntas 1,2,3.
- Conjunto/opción 2: Responder a las preguntas 1,2,4.
- Conjunto/opción 3: Responder a las preguntas 1,3,4.
- Conjunto/opción 4: Responder a las preguntas 2,3,4.
Como podemos ver, el estudiante puede formar 4 conjuntos (n) de 3 elementos (x). Por lo tanto, la combinatoria sin repetición nos dice cómo formar o agrupar una cantidad finita de datos/observaciones, en grupos de una cantidad dada sin que ninguno de los elementos se repita en cada grupo. Esta es la principal diferencia entre la combinatoria con repetición (los elementos pueden repetirse en cada grupo) y la combinatoria sin repetición (ningún elemento puede repetirse en cada grupo).
¿Cómo calcular la combinatoria sin repetición?
La fórmula de la combinatoria sin repetición es:
n = Observaciones totales
x = Número de elementos seleccionados
Ejemplo de combinatoria sin repetición
Imaginemos un pelotón militar de 12 soldados. El capitán del ejército quiere formar grupos de 2 soldados para infiltrarse detrás de las líneas enemigas en diferentes puntos, ¿cuántos grupos diferentes podría formar?
Para resolver el problema, primero tenemos que identificar el número total de elementos. En este caso hay 12 soldados en total, así que ya tenemos nuestra n. Como el capitán quiere grupos de 2, ya sabemos cuál es nuestra x. Sabiendo esto, podríamos sustituir en la fórmula y tener el número de combinaciones de grupos de 2.
n = 12
x = 2
Aplicando el factorial para el denominador tendríamos 12*11*10*…*1 = 479.001.600. Para el denominador tenemos 2*1*10*9*8…*1 = 7.257.600. Nuestro número combinatorio es =479.001.600/7.257.600 = 66.
Como vemos, el capitán puede formar 66 parejas distintas de soldados de entre los 12 que dispone.
Contenido