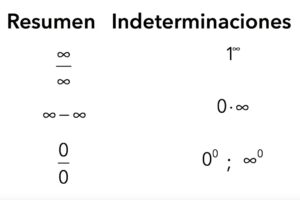
¿Qué son las ecuaciones matriciales?
Las ecuaciones matriciales son como las ecuaciones normales, pero en lugar de estar formadas por números, están formadas por matrices. Por ejemplo:
Por lo tanto, la solución X también será una matriz.
Como saben, las matrices no pueden ser divididas. Por lo tanto, NO PUEDES despejar la matriz X pasando a dividir la matriz que la multiplicó al otro lado de la ecuación:
Hay todo un procedimiento a seguir para limpiar la matriz X. Así que vamos a ver cómo limpiar las ecuaciones matriciales con un ejercicio resuelto:
Cómo resolver ecuaciones matriciales. Ejemplo
- Resuelve la siguiente ecuación matricial:
Lo primero que debemos hacer es despejar la matriz X. Así que pasamos restando la matriz B del otro miembro de la ecuación:
Para terminar de limpiar la matriz X, tenemos que pasar al otro miembro de la matriz de la ecuación A. Sin embargo, no podemos pasarla dividiendo como siempre lo hicimos en las ecuaciones normales, porque las matrices no pueden ser divididas. Pero debemos hacer lo siguiente:
Tenemos que multiplicar los dos miembros de la ecuación por el inverso de la matriz que está multiplicando la matriz X y, además, multiplicar los dos miembros por el lado donde está la matriz.
En este caso, la matriz que multiplica X es A, y está en su lado izquierdo. Por lo tanto, multiplicamos los dos miembros de la ecuación por el inverso de A (A-1):
Una matriz multiplicada por su inversa es igual a la matriz identidad. Por tanto
Cualquier matriz multiplicada por la matriz identidad da como resultado la misma matriz. Por tanto:
Calculamos la adjunta de la matriz A:
Y una vez hallada la matriz adjunta, se procede a calcular la matriz transpuesta para así determinar la matriz inversa:
Ahora sustituimos todas las matrices en la expresión para calcular X:
Y procedemos a resolver las operaciones con matrices. Primero calculamos el paréntesis haciendo la resta de matrices:
Y, finalmente, multiplicamos las matrices:
Contenido