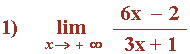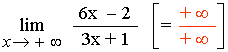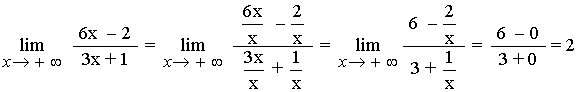
Límite infinito entre infinito

A veces, al calcular los límites encontramos ciertas expresiones cuyos valores no conocemos a priori. Estas son las llamadas indeterminaciones. Para algunas de ellas existen reglas que nos permiten calcular su valor (como en el caso de 1 ∞ ). Pero la mayoría de las indeterminaciones no se resuelven de forma tan directa, sino que debemos realizar una serie de operaciones o cálculos para determinar sus valores.

Límite infinito

Donde, lim es la forma abreviada de escribir límite, x → a se lee "cuando x tiende al valor a en la función", es decir, cuando la variable x toma valores muy cercanos al valor a y L es el resultado del límite.

Muchas veces queremos saber cómo se comporta una función en el infinito, en algunas ocasiones es algo complejo, incluso abstracto. Para considerar un límite de una función en el infinito tenemos que tener en cuenta una serie de reglas que nos ayudarán a facilitar las operaciones:

∞ + ∞ = ∞, un número muy grande sumado a otro, nos dará como resultado un número inmensamente grande.
∞ - ∞ = indeterminado, como no conocemos exactamente el tamaño de los infinitos no podremos conocer el resultado de esta resta, por lo tanto, es indeterminado.
± ∞ ± k = ± ∞, cualquier número que se sume o se reste a un número inmensamente grande (negativo o positivo), no afectará al número gigante independientemente de su signo.
± k × ± ∞ = ± ∞, a partir de la regla de los signos de la multiplicación, podemos decir que cualquier número, excepto el cero, multiplicado por el infinito será infinito.
± ∞ × ± ∞ = ± ∞, a partir de la regla de los signos de la multiplicación, podemos decir que un número gigante por otro, será igual a otro número inmensamente grande.
(± ∞) / (± ∞) = indeterminado, como no tenemos con precisión el valor de los infinitos, esta división nos da un número indeterminado.
k / (± ∞) = 0, cualquier número conocido dividido por el infinito será igual a cero; una analogía sería dividir un pastel en un millón de personas, podemos decir que nada tocará a cada una de ellas.
0 × ± ∞ = indeterminado, es imposible saber si en el infinito la multiplicación por cero es algo determinado, por eso lo tomamos como indeterminado.