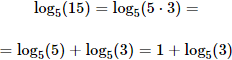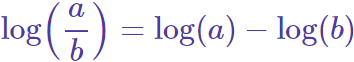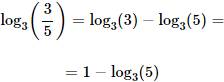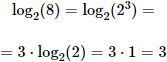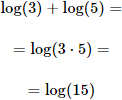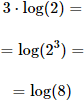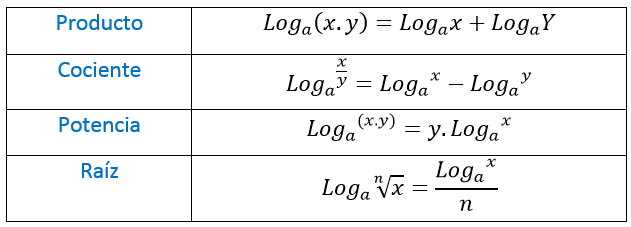
Propiedades de los logaritmos
Necesitamos recordar la definición de logaritmo: El logaritmo en base b de un número a está representado por logb(a) y es el número c el que cumple bc = a. Donde: El número b es la base del logaritmo. Tiene que ser un real positivo distinto de 1. El número a es el argumento del logaritmo. El número c es el logaritmo en base b de a. Si se entiende, no es necesario escribir la base.
Propiedades de los logaritmos
Logaritmo de un producto
El logaritmo de un producto de factores es la suma de los logaritmos de los factores:
Ejemplo:
Logaritmo de un cociente
El logaritmo de un cociente es el logaritmo del numerador menos el logaritmo del denominador:
Ejemplo:
Logaritmo de una potencia
El logaritmo de una potencia es el logaritmo de la base de la potencia multiplicado por el exponente:
Ejemplo:
Ejemplo:
Podemos sumar logaritmos con base común:
No podemos sumar logaritmos con base distinta:
Ejemplos de aplicación
Ejemplo 1
Solución:
La suma de logaritmos es el logaritmo del producto:
Ejemplo 2
Solución:
El número 3 pasa al argumento como un exponente:
Contenido