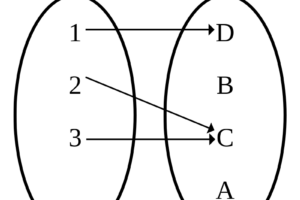
Variaciones
La combinatoria es mucho más divertida de lo que parece. Son técnicas de conteo que están al alcance de todos. La combinatoria es el arte de contar números
La combinatoria es una rama de las matemáticas con mucho potencial. En menos de un minuto es capaz de resolver preguntas aparentemente complejas. Básicamente analiza las diferentes formas de hacer agrupaciones con los elementos de un conjunto, de formarlos y de calcular su número.
Los problemas combinatorios siempre han atraído la atención de los matemáticos. Uno de los más famosos es el problema de los cuadrados mágicos. También es muy famoso el triángulo de Pascal, que además de tener propiedades impresionantes, la disposición de sus números coincide exactamente con los números combinatorios.
Pero fue el genio Leonhard Euler quien desarrolló a principios del siglo XVIII una verdadera escuela de matemáticas combinatorias.
Combinatoria. Técnicas de recuento
Principio de multiplicación
Se utiliza cuando tenemos n1 opciones de escoger un objeto, n2 opciones de escoger un segundo objeto, n3 opciones de escoger un tercer objeto etc. Matemáticamente podemos representarlo así: n1·n2·n3· …nn
Una marca de coches comercializa un modelo en tres versiones (3 puertas, 5 puertas y familiar). El motor puede ser de dos tipos (diesel o gasolina). Hay cuatro colores disponibles. ¿Cuántos tipos diferentes de coches se hacen para este modelo?
Aplicando el principio de multiplicación tenemos que 3·2·4 = 24 coches diferentes
Variaciones ordinarias o sin repetición
Ocho corredores participan en una carrera atlética. ¿De cuántas maneras se pueden otorgar las tres medallas?
La medalla de oro puede ser obtenida por los ocho corredores (aunque haya favoritos), con la de plata tenemos 7 posibilidades, y con el tercer lugar sólo 6.
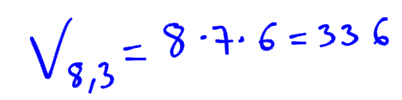
Es decir, tenemos variaciones ordinarias de 8 elementos tomados 3 a la vez.
En general, llamamos variaciones ordinarias de m elementos tomados de n en n (n≤m), a los diferentes grupos que se pueden formar con m elementos de tal manera que
- En cada grupo n elementos diferentes entran
- Influye en el orden de colocación
Generalizando, lo hemos hecho:

El factorial de un número (n!) es el producto de los primeros n números naturales. Por ejemplo 5! = 5-4-3-2-1
En general:
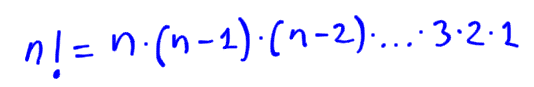
Esto es un número combinatorio:
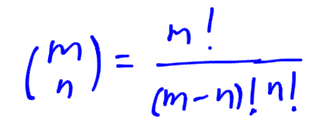
Variaciones con repetición
¿Cuántos números de tres dígitos pueden formarse con los dígitos? 1, 2, 3, 4, 5 ?
En este caso tenemos que m = 5 y n = 3
No todos los elementos encajan. Sólo se introducen 3 dígitos de 5 dígitos.
El orden es importante. Son números diferentes: 123, 231, 321.
Si los elementos se repiten.
En general, llamamos variaciones con repetición de m elementos tomados de n en n, a los diferentes grupos que se pueden formar con m elementos para que

En el caso que nos ocupa,tenemos que VR5,3 = 5·5·5= 125 Fíjate que tenemos 3 factores
Permutaciones ordinarias
Imagina que vas al cine con 5 amigos. Te sientas en seis asientos consecutivos de una sola fila. ¿De cuántas maneras diferentes puedes sentarte?
¡720 maneras diferentes! Sorprendente, ¿no?
En el primer asiento puedes sentar a 6 personas, 5 en el segundo, 4 en el tercero, etc. Matemáticamente hay 6-5-4-3-2-1= 720 posibilidades. Esto está representado por el factorial 6 (6!)
Todos los elementos están involucrados en las permutaciones y sólo varía el orden de colocación.

Cuando la permutación es circular, reducimos el número de elementos en 1. En este caso se reduce a 5!=5-4-3-2-1 = 120 En general, tenemos que hacerlo:
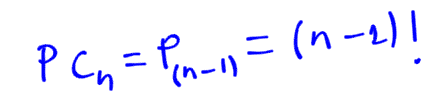
Es bien sabido que la disposición de los comensales en una mesa puede plantear problemas más interesantes de lo que parece a primera vista.
Permutaciones con repetición
Un jugador de ajedrez quiere pedir 5 peones negros y 3 blancos en una fila. ¿De cuántas maneras diferentes puede hacer esto?
En este caso los elementos se repiten. Es una permutación de 8 objetos donde 5 se repiten, y 3 se repiten. En estas ocasiones podemos expresarlo así:

Si comprendes lo que te pide el problema, entenderás la fórmula anterior. Pero por si acaso, aquí tienes la fórmula general para resolver cualquier problema de permutaciones con repetición.
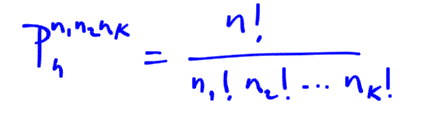
Contenido