Funciones convexas
Definimos una función convexa (cóncava hacia arriba) como una función que está siempre por debajo de las líneas que unen dos puntos cualesquiera de ella. Formalmente, diremos que una función es cóncava hacia arriba en un intervalo
si para todo

Definidas de esta forma, podemos notar además, que las funciones convexas siempre estarán por encima de cualquier recta tangente a la curva que definen. Formalmente, si es un punto del intervalo
, entonces

Es notable que la pendiente de las líneas tangentes a las funciones convexas tienen una tendencia creciente, al menos en el gráfico que hemos expuesto se puede observar con claridad que como valor de , estas pendientes pasan de ser negativas (inclinadas hacia abajo) a ser positivas (inclinadas hacia arriba).
Funciones cóncavas
Definimos una función cóncava (cóncava hacia abajo) como una función que está siempre por encima de las líneas que unen dos puntos cualesquiera de ella. Formalmente, diremos que una función es cóncava hacia abajo en un intervalo
si para todo

Definido de esta manera, también podemos notar que las funciones cóncavas siempre estarán por debajo de cualquier línea recta tangente a la curva que definen. Formalmente, si es un punto del intervalo
, entonces
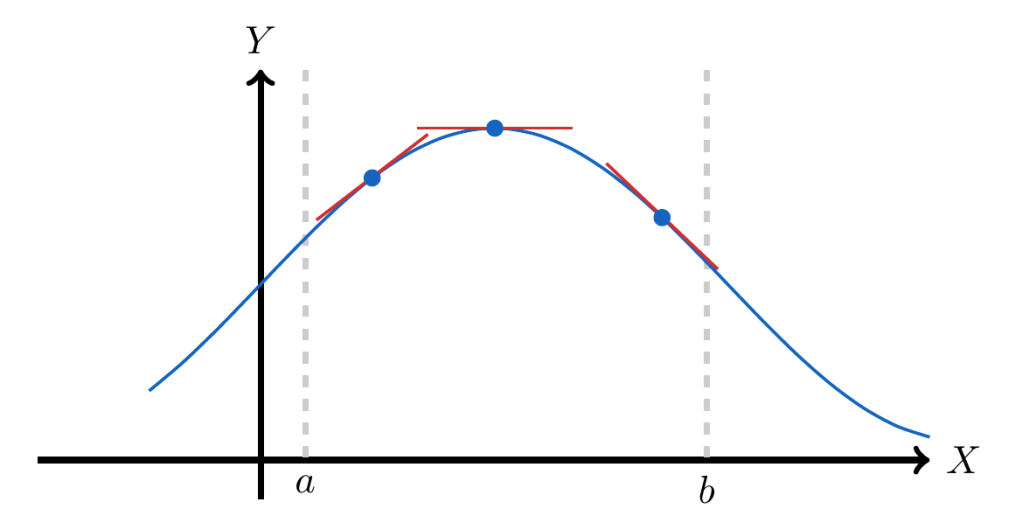
Es notable que la pendiente de las líneas tangentes a las funciones cóncavas tienen una tendencia decreciente, al menos en el gráfico que hemos expuesto se puede observar con claridad que como valor de , estas pendientes pasan de ser positivas (inclinadas hacia arriba) a ser negativas (inclinadas hacia abajo).