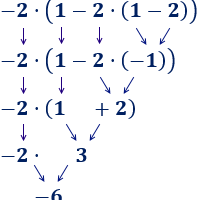
Teorema del valor medio
El Teorema del Valor Medio o Teorema de Lagrange afirma que si una función f(x) es continua en un intervalo cerrado [a, b], hay al menos un punto (que es derivable) perteneciente al intervalo abierto c ∈ (a, b), en el que se cumple que
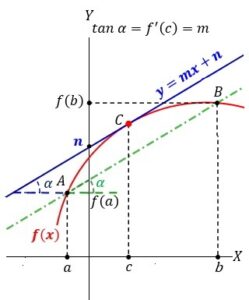
Gráficamente:
Como la derivada de una función en un punto es la tangente del ángulo α que forma la línea tangente en ese punto, las tangentes de los ángulos de las dos líneas, la línea secante a través de AB y la línea tangente en el punto (c, f(c)) son paralelas y la tangente de ambas es f'(c).
El teorema del valor medio es una generalización del teorema de Rolle, ya que no requiere que los extremos del intervalo sean iguales.
Teorema del valor medio ejemplos
- Demuestra que una raíz de la función:
está en el intervalo 
Vamos a evaluar la función en los extremos del intervalo:
Como 
es negativo, 
es positivo y la función es continua, dado que el denominador nunca se hace cero, una de sus raíces está en el intervalo .
- Demuestra que la ecuación
tiene una solución en el intervalo
.
Evaluamos la función 
en 
y 
:
Entonces, por el teorema de valor intermedio, haciendo 
, 
y 
, existe un número 
en tal que 
.
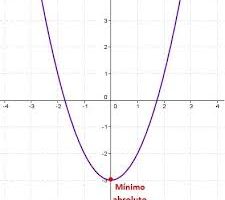
Para cualquier función continua en el rango [a,b], f(x0) es un número finito. Es decir, hay un número finito M que es el valor máximo que toma la función para algún valor xM. Lo mismo puede decirse del mínimo: hay un valor xm tal que f(xm) = m siendo m el valor mínimo que toma la función en el intervalo [a,b]. Esto es lo que se refleja en el siguiente teorema.
Contenido
