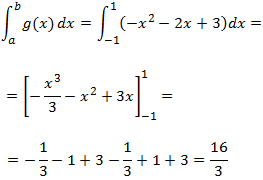
Integral definida
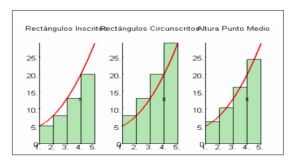
¿Cómo podemos acercarnos al área de una región limitada por el gráfico de una función positiva, el eje de abscisas y dos líneas verticales, calculando las áreas de una serie de rectángulos que delimitan el valor que buscamos? Tenemos dos tipos de dimensiones: una superior (o exceso) a la que hemos llamado la suma superior (Sn) y una inferior (o defecto) a la que hemos llamado la suma inferior (sn), de modo que si llamamos A al valor del área buscada se cumple
sn< A < Sm
donde n y m son dos números naturales cualquiera. En el ejemplo anterior, además, para el mismo valor n, la diferencia entre la suma superior y la suma inferior Sn-sn tiende a cero cuando n tiende al infinito. Esto último no es cierto en general con ninguna función, aunque sí lo es mientras la función de partida sea continua en el intervalo en el que se calcula el área.
Integral definida: interpretación gráfica
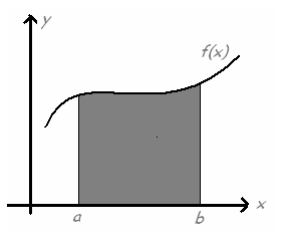
El concepto de integral definida está relacionado con el valor que determina el área bajo la curva dada por una función f (x) en el intervalo [a,b].
Uno de los primeros pasos para llegar a este concepto fue desarrollado por Riemann, que abordó el cálculo del área con particiones rectangulares, como se muestra en el siguiente gráfico.
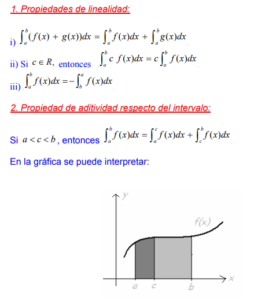
Propiedades de la integral definida
Que f, g sean funciones integrables definidas en el intervalo [a, b]. Entonces se cumplen las siguientes propiedades:
Cómo resolver una integral definida
∫(2)(-1)[x+2*] dx =
Derivar las partes que viene en la función:
- [∫x(dx) +∫2(dx)](2)(-1)
En la primera parte tenemos que derivar a "x" pero entonces utilizaremos la derivada de x^(n)
y la formula es x^(n) = x^(n+1)/(n+1)
Ahora una vez que ya tenemos la formula, aplicamos x^(1+1)/(1+1) = x^2/2
- Tenemos que ∫2(dx) la constante es "2" la sacamos fuera de la integral y nos quedaría así= 2∫(dx).
- Integramos y nos quedará así: 2x
[x(^2)/(2) + 2(x)] (2)(-1)
- tendremos que sustituir a x por 2 y x por (-1)
Regla de Barrow
La regla de Barrow establece que la integral definida de una función continua f(x) en el intervalo [a, b] es igual a la diferencia entre los valores que toma una función primitiva F(x) de f(x), en los extremos de ese intervalo.
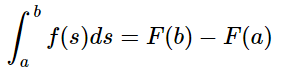
Para resolver una integral definida de una función, basta con encontrar una primitiva de la función y sustituir en ella los límites superior e inferior de integración y restar ambos valores.
Contenido