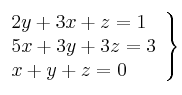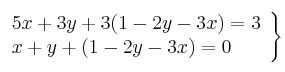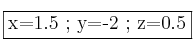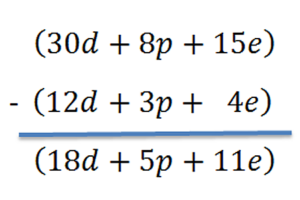Ejercicios de sistemas de ecuaciones 3x3

Se llama sistema de ecuaciones lineales a un conjunto de ecuaciones lineales referidas todas ellas a las mismas incógnitas. Un sistema 3×3 significa 3 ecuaciones con 3 incógnitas. La solución de un sistema de ecuaciones lineales es el conjunto de valores que verifican todas y cada una de las ecuaciones.

Sistemas de ecuaciones 3x3

Las ecuaciones pueden tener más de una o dos variables. Encontrarás ecuaciones que tienen tres variables. Las ecuaciones con una variable se trazan en una línea. Las ecuaciones con dos variables se trazan en un plano. Las ecuaciones con tres variables se dibujan en un espacio tridimensional.

Las ecuaciones con una variable requieren sólo una ecuación para tener una solución única. Las ecuaciones con dos variables requieren dos ecuaciones para tener una sola solución (un par ordenado). Por lo tanto, no debería sorprendernos que las ecuaciones con tres variables requieran un sistema de tres ecuaciones para tener una única solución (un par ordenado).

Resolviendo un sistema de tres variables

Elige dos ecuaciones y úsalas para eliminar una variable.
Elija otro par de ecuaciones y úselas para eliminar la misma variable.
Usa el par de ecuaciones resultante para eliminar una de las otras variables.
Resuelve la ecuación final para la variable restante.
Encuentra el valor de la segunda variable. Usar una de las ecuaciones resultantes de los pasos 1 y 2 y el valor encontrado en el paso 4.
Encuentra el valor de la tercera variable. Usando una de las ecuaciones originales y los valores encontrados en los pasos 4 y 5.
Comprueba tu solución en las tres ecuaciones.

Entrada Relacionada: Vector components

Ejercicios de sistemas de ecuaciones 3x3

Despejaremos "z" en la primera ecuación

La expresión obtenida la sustituimos por "z" en las demás ecuaciones:

Nos queda un sistema de 2 ecuaciones con 2 incógnitas.
Eliminamos los paréntesis, ordenamos las ecuaciones y resolvemos el sistema.
Obtenemos como soluciones y