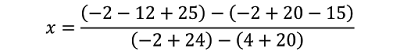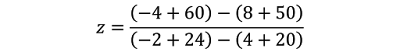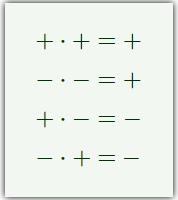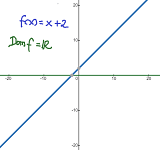
Método de cramer paso a paso

La regla de Cramer proporciona la solución de sistemas de ecuaciones lineales compatibles determinados (con una única solución) mediante el cálculo de determinantes. Es un método muy rápido para resolver sistemas, especialmente para sistemas de 2×2 y 3×3 dimensiones.

Método de cramer paso a paso

Resolver el siguiente sistema de ecuaciones con el método de Cramer

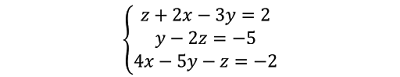
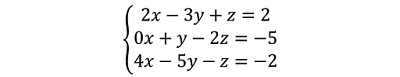
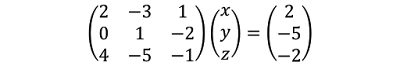
Ordenamos las ecuaciones según Ax+By+Cz=D.

Escribimos el sistema de ecuaciones en forma de matriz. Es decir, en cada fila indicamos los coeficientes de cada ecuación. Luego se multiplica por una matriz con las variables. Luego la igualamos con una matriz con los términos independientes.

Aplicamos a Cramer, para encontrar el valor de x.

Para ello proponemos una división, donde el dividendo es un determinante con la matriz que contiene los coeficientes de las ecuaciones. Pero, la primera columna es cambiada por la matriz que contiene los términos independientes. Además, añadimos las dos primeras columnas a la izquierda del determinante.

En el denominador, indicamos un determinante con la matriz que contiene los coeficientes de las ecuaciones. Añadimos las dos primeras columnas de esta matriz a la derecha.

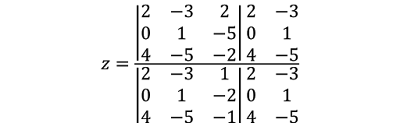
Para calcular el numerador, primero multiplicamos los elementos de cada diagonal que se indican en azul y se suman en un primer paréntesis. Luego, indicamos un segundo paréntesis precedido por el signo menos (-) con la multiplicación de los elementos de cada diagonal que se indican en color rojo y se suman.

De la misma manera, procedemos en el denominador.