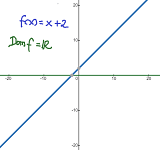
Cómo se calcula el dominio de una función
Siempre es interesante encontrar (si es que hay) estos casos. Hay que ver qué operaciones hay que hacer para encontrar los valores que no tienen imagen, que hacen que la función no exista. Estos son los casos más comunes:
- Es imposible dividir por cero
- El resplandor de una raíz con índice uniforme no puede ser negativo
- El logaritmo de cero o un número negativo no existe
El dominio de una función polinómica
Suelen ser los favoritos de cualquier estudiante porque no dan ningún problema. Su dominio es el valor de todos los números reales. En ellos no encontrarás raíces o denominadores que te compliquen la vida. Ejemplo:
f(x)=x3+5x2-1
En otras palabras, en las funciones polinómicas no hay valores de x para los que no exista f(x), es decir, la función siempre existirá. Decimos entonces que su dominio es el conjunto de todos los números reales:
Domf=R
Dominio de una función racional
El dominio de estas funciones será R, excepto los valores que anulan el denominador. En estos casos, para obtener el dominio de una función racional, hay que buscar el valor o valores que hacen que el denominador sea cero. Estos valores no pertenecerán al dominio. Ya has visto un ejercicio resuelto anteriormente. Les muestro un ejemplo más:
f(x)=3x-7 Domf={R-7}
Es decir, la función existirá mientras x sea diferente de 7, por lo que el dominio es el conjunto de todos los reales excepto el número primo 7.
Calcular el dominio de una función irracional
¿Qué es una función irracional? Es aquella en la que aparece una raíz. Porque las raíces no pueden ser puestas en forma racional o fraccionada. El mismo Pitágoras tuvo dificultades con esto.
Aquí hay que distinguir entre dos casos diferenciados.
- Raíz de índice impar. Siempre existen. Su dominio es R
- Raíces de índice de paridad. Existirán siempre y cuando su raíz sea igual o mayor que cero
Dominio de una función logarítmica
Recuerde que las funciones logarítmicas son las que contienen la x dentro de un logaritmo.
Estas funciones siempre existirán cuando el logaritmo sea mayor que 0. Los otros valores serán los que hagan que el logaritmo sea cero o negativo. Y estos valores son los que hay que excluir del dominio de la función.
Contenido