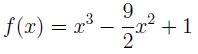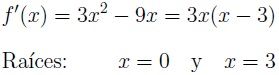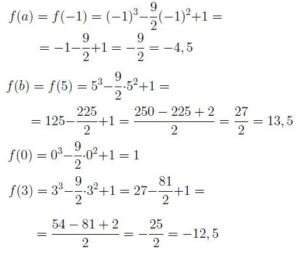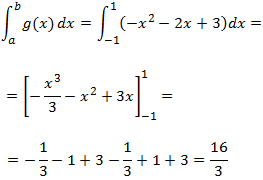Calculadora de máximos y mínimos

Los máximos y mínimos de una función son los valores más grandes o más pequeños de esa función, ya sea en una región o en todo el dominio. Los máximos y mínimos de una función f son los valores más grandes (máximos) o más pequeños (mínimos) que toma la función, ya sea en una región (extremos relativos) o en todo su dominio (extremos absolutos).

Teorema de los valores extremos

Una función f(x) continua en un rango cerrado [a,b] siempre tiene un máximo absoluto y un mínimo absoluto en ese rango.

No se garantiza que haya extremos absolutos si se definen en un intervalo abierto.

Este teorema confirma la existencia de un máximo absoluto y un mínimo absoluto en una función continua definida en un intervalo cerrado [a,b], pero no define cómo se calcula. Para calcularlos el procedimiento es el siguiente:

Derivar la función, obteniendo f '(x).
Encontrar las raíces de la derivada, es decir, los valores de x de tal manera que la derivada sea 0.

Supongamos que las raíces de f ' son {r1, r2,...,rn}.

Se calcula la imagen de los extremos del intervalo (f(a) y f(b)). También se calcula la imagen de las raíces ( f(r1) , f(r2) ,..., f(rn)).
El máximo y mínimo absoluto de f será:

Ejemplo

Encuentra el máximo y el mínimo absoluto de la función f(x) en el rango [-1.5], de tal manera que

Aplicaremos el procedimiento del teorema de los extremos.

Derivamos la función, obteniendo:

Encontramos las raíces de la derivada:

Las imágenes de los extremos del intervalo y de las dos raíces son

Por lo tanto, el máximo y mínimo absoluto de f será

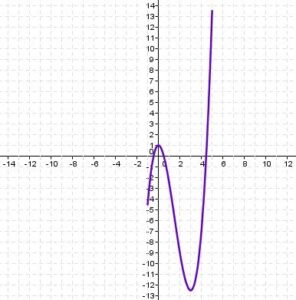
Entrada Relacionada: Ejercicios de variaciones

Se han comparado cuatro imágenes de la función en cuatro puntos, las dos en las que el valor de la derivada es cero (0, 1) y (3, -12,5) con las correspondientes a los extremos del intervalo (-1, -4,5) y (5, 13,5). Resultado: máximo absoluto en el punto (5, 13,5) y mínimo absoluto en el punto (3, -12,5).

Contenido