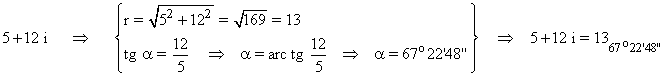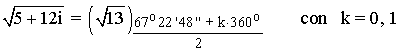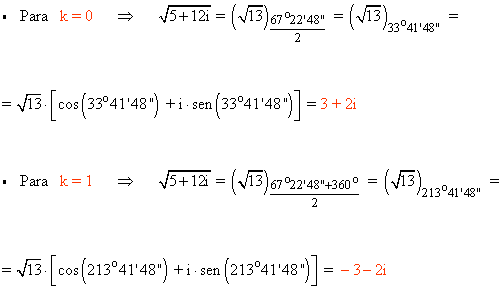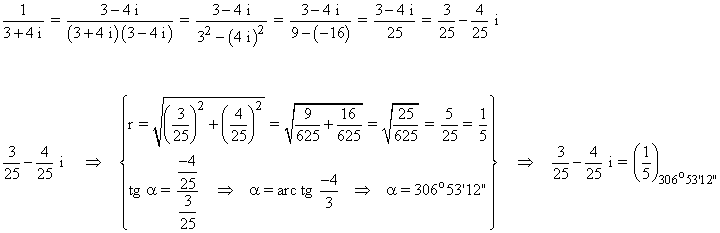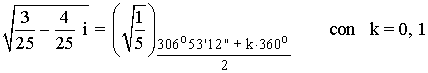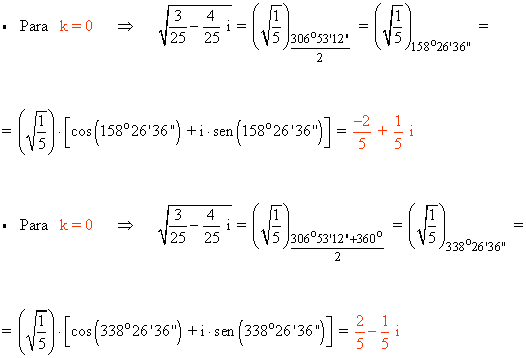Raíces de números complejos ejercicios resueltos
Un número complejo es la suma de un número real y un número imaginario. Un número imaginario es la raíz cuadrada de un número negativo. √-4=2·√-1=2i es la unidad imaginaria La unidad imaginaria es la raíz de menos uno. El teorema fundamental del álgebra, que utilizaremos más adelante, dice que cada polinomio tiene el número de soluciones reales o complejas igual al grado de ese polinomio.
Raíces de números complejos ejercicios resueltos
Hallar la raíz cuadrada de los siguientes números complejos:
a) 5 + 12 i b) 1 / (3 + 4 i)
a) 5 + 12 i
En primer lugar pasamos el número complejo a forma polar:
Como el afijo es (5, 12) el ángulo del número complejo está en el primer cuadrante..
A continuación aplicamos la fórmula para encontrar las raíces cuadradas:
b) 1 / (3 + 4 i)
En primer lugar pasamos el número complejo a forma polar:
Como el afijo es (3/25, -4/25) el ángulo del número complejo está en el cuarto cuadrante..
A continuación aplicamos la fórmula para encontrar las raíces cuadradas: