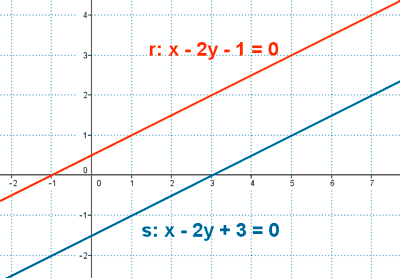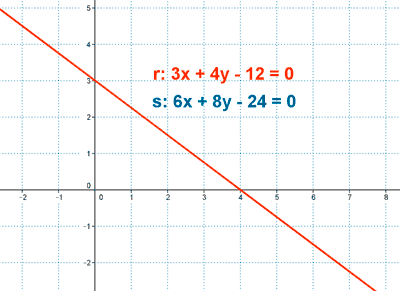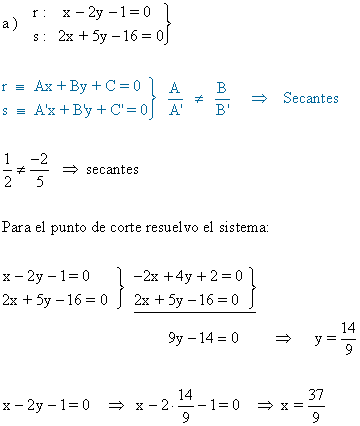
Posición relativa de dos rectas
En el espacio, hay cuatro posiciones relativas que pueden tomar dos líneas. Estas posiciones se llaman líneas coincidentes, paralelas, secantes e intersecantes. Para entender esto claramente supongamos que tenemos dos líneas, que serán r y s que se presentarán dadas como intersección de dos planos. Si lo que queremos es determinar la posición relativa de éstas en el espacio, lo que debemos hacer es analizar el sistema formado por las ecuaciones de los cuatro planos.
Posición relativa de dos rectas
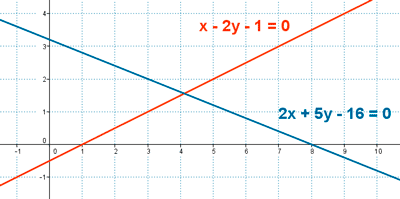
Rectas secantes
Dos rectas son secantes si tienen un punto en común. Para hallar el punto común de las dos rectas basta con resolver el sistema formado por ambas ecuaciones.
Rectas paralelas
Dos rectas son paralelas si no tienen ningún punto en común, y lo representamos por ||
Rectas coincidentes
Dos rectas son coincidentes si son la misma recta.
Resumen de la posición relativa de dos rectas
| Secantes | El sistema tiene una única solución | |
|---|---|---|
| Paralelas | El sistema no tiene soluciones | |
| Coincidentes | El sistema tiene infinitas soluciones | |
Ejemplo de Posición relativa de dos rectas
Contenido