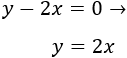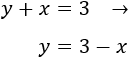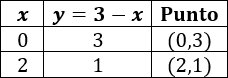
Qué es el método gráfico de un sistema de ecuaciones
Este método es uno de los más cómodos cuando tenemos acceso a un ordenador con un plotter, o cuando el dibujo y los gráficos se nos dan maravillosamente. Aquí aprovechamos la propiedad de representación de una recta para "dibujar" o representar cada una de las ecuaciones del sistema de ecuaciones en el plano cartesiano. En este método suele haber tres casos con estas dos líneas y dependiendo de cada caso y de cuál nos toque, sabremos si nuestro sistema de ecuaciones tiene una solución, más de una solución o ninguna.
Pasos para resolver un sistema de ecuaciones por el método gráfico
Para resolver un sistema de ecuaciones mediante el método gráfico se realizan los siguientes pasos:
- Despeja incógnitas en ambas ecuaciones.
- Construye la tabla de valores correspondientes para cada una de las dos funciones de primer grado obtenidas.
- Representar gráficamente en los ejes de coordenadas.
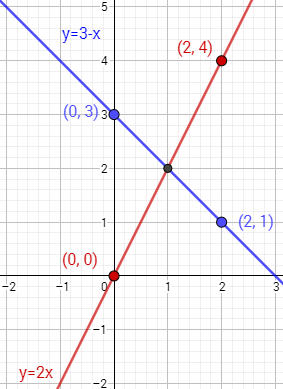
Como vamos a trabajar con sistemas de dos ecuaciones lineales con dos incógnitas (x e y), el gráfico de cada ecuación es una línea. Como resultado, la intersección de las gráficas es un solo punto (a, b) y la solución del sistema es x = a y y = b. Sin embargo, si las líneas son paralelas (no cortadas), el sistema no tiene solución, y si son iguales hay infinitas soluciones.
Para aplicar el método gráfico debemos saber cómo representar los gráficos de las líneas.
Ejemplo de un sistema de ecuaciones resuelto por el método gráfico
Resolución
Lo primero que hacemos es aclarar la y en ambas ecuaciones.
Primera ecuación:
Segunda ecuación:
Ahora vamos a calcular algunos puntos de las dos funciones para representarlas. Usamos, por ejemplo, x = 0 y x = 2.
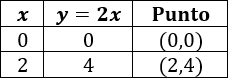
Para la primera función tenemos la tabla
Para la segunda función tenemos la tabla (usando los mismos valores para x):
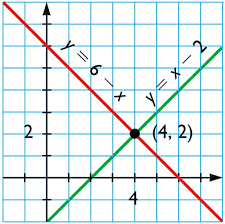
Representamos los puntos de la tabla y los unimos:
La solución del sistema es el punto donde se cortan las gráficas:
Contenido