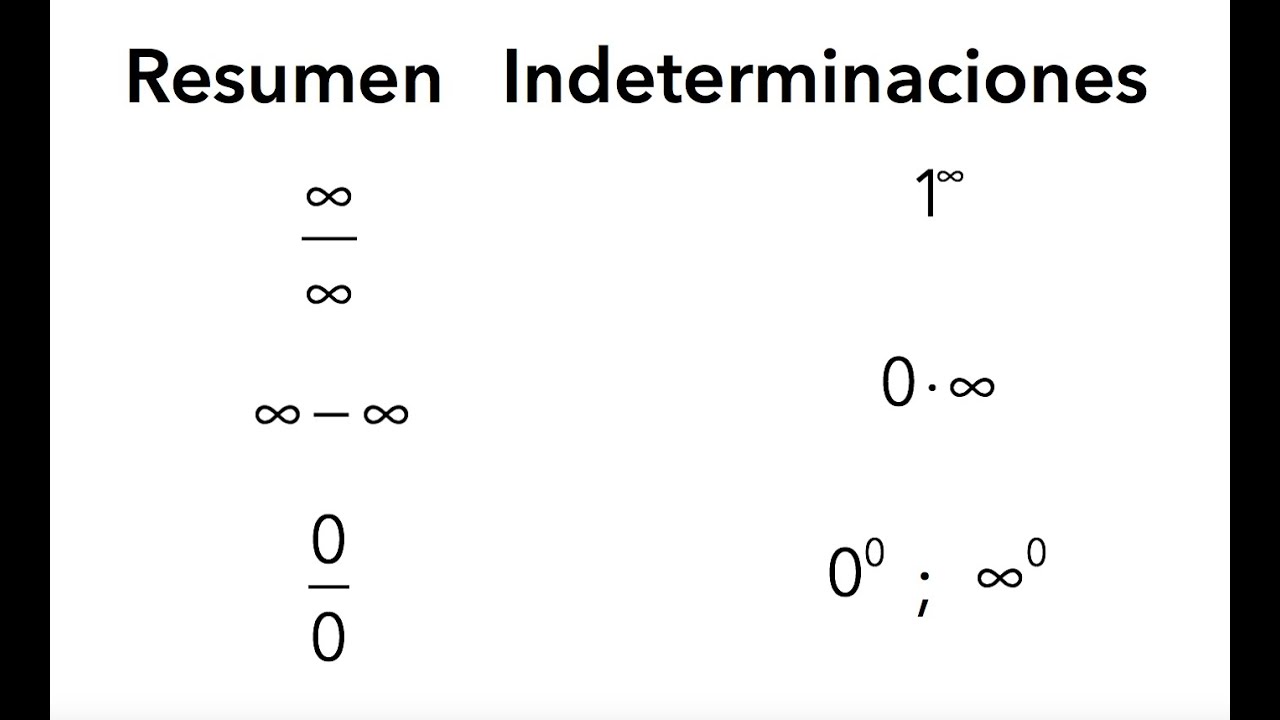
Indeterminaciones límites

Al calcular los límites de las funciones nos encontraremos a menudo con expresiones cuyo resultado no puede determinarse directamente utilizando las propiedades habituales de los límites de las funciones. En estos casos, el resultado del límite dependerá de la función concreta que estemos estudiando.

Indeterminación

Muchas veces la resolución de los límites no puede hacerse por el método de evaluación tradicional. En esos casos, es aconsejable utilizar primero el método de evaluación tradicional para determinar a qué tipo de indeterminación nos enfrentamos.

Intentemos comprender por qué son indeterminaciones, es decir, expresiones cuyo resultado no puede conocerse de antemano ya que depende de las funciones que intervienen en el límite.

Como hemos comentado anteriormente, el principal error que se suele cometer es considerar "∞" como un número real y tratar de operar con él como si lo fuera.

Por ejemplo, es muy común creer que "∞-∞" es siempre 0, ya que lo consideramos como un número real, pero no lo es. Recordemos que cada vez que aparece el 0 como resultado de un límite, debemos sustituirlo por la expresión "números tan pequeños como queramos" y cuando aparece "∞", debemos sustituirlo por "números tan grandes como queramos".

De esta manera, "∞-∞" se interpreta como "un número muy, muy grande" menos "otro número muy, muy grande". Pero, ¿cuál de los dos números es más grande?

Ahí es donde entran las diferentes posibilidades:

Si el primero es más grande (de orden superior), la diferencia será muy grande y positiva, y el resultado tenderá a "+∞".
Si es más grande (de orden superior) el segundo, la diferencia será muy grande pero negativa, y el resultado tenderá a "-∞".
Pero si ambos son muy grandes del mismo orden, la diferencia puede tender a un número real.

Entrada Relacionada: Cómo se obtiene el mínimo común múltiplo

Como se puede ver, la misma expresión da lugar a diferentes resultados dependiendo de la función que se esté considerando. Por eso se llama "indeterminación".