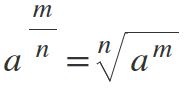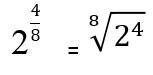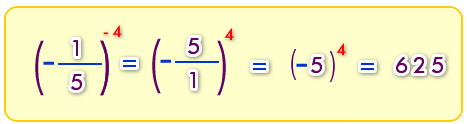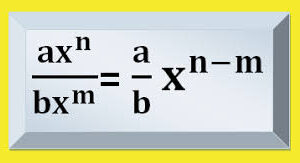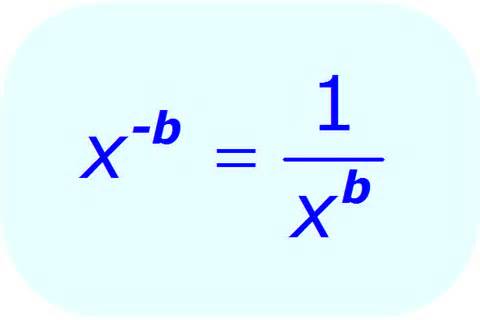
Exponentes fraccionarios negativos
Toda potencia de exponente fraccionario y positivo es igual al radical cuyo índice es el denominador del exponente, y cuya raíz es la base de la potencia elevada a un exponente igual al numerador del exponente dado.
Exponente fraccionario
Si la potencia tiene una fracción como exponente, esto se resuelve transformándola en una n-ésima raíz, donde el numerador permanece como exponente y el denominador representa el índice de la raíz:
Ejemplo
Propiedad de Exponente Fraccionario y Exponente Negativo
Potencia del exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción no es irreducible, y en la que se cumple:
Potencia del exponente negativo
Una potencia que tiene un exponente negativo se desplaza y por lo tanto su exponente cambiará automáticamente a uno positivo:
a − b = 1 / ab
Ejemplo de Exponentes fraccionarios negativos
Una potencia con exponente negativo y base distinta de cero, es igual a una fracción con el numerador 1 y con el denominador igual a la potencia con exponente positivo.
Para calcular el valor de una fracción con exponente negativo, se intercambian el numerador y el denominador, y el signo del exponente se deja positivo.
Contenido