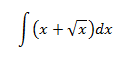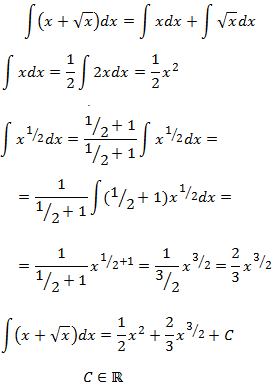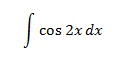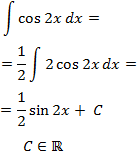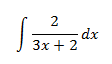
Fórmulas de integrales
Las integrales directas o inmediatas son las integrales que por su sencillez no requieren la aplicación de un método de integración para su resolución. Para resolver estas integrales necesitamos conocer las derivadas de las funciones elementales, la regla de la cadena y las propiedades de las integrales.
Fórmulas de integrales
Integrales inmediatas ejercicios resueltos
Ejercicio 1
Como tenemos una suma en el integrando, podemos descomponer el integrando como una suma integral. Además, escribimos la raíz cuadrada como una potencia:
Ejercicio 2
Si escribimos un 2 en el integrando, tendremos la derivada sinusoidal del doble ángulo:
Ejercicio 3
Normalmente, las integrales inmediatas de las funciones racionales se derivan de un logaritmo. Si no, tendremos que aplicar otros métodos para las integrales de las funciones racionales.
La integral será la derivada de un logaritmo si conseguimos escribir el numerador como la derivada del denominador. Para ello, en esta integral, debemos cambiar el 2 por un 3:
Contenido