Derivadas de funciones

La derivada de una función f(x), o función derivada de f(x), es esa función, denotada f'(x), que asocia a cada x la velocidad de cambio de la función original f(x) en ese punto, es decir, su tasa de variación instantánea. Las derivadas son herramientas fundamentales en todas las ciencias, incluida la física.

Función derivada

Llamamos derivadas elementales o inmediatas a las derivadas de las funciones elementales (por ejemplo, la función constante, la potencia, el coseno, la exponencial, el logaritmo, etc.).

Las funciones más complejas pueden escribirse como composiciones de funciones elementales. Podemos derivar estas funciones más complejas utilizando las reglas de derivación, la regla de la cadena y las derivadas elementales.

Las derivadas elementales se calculan con la propia definición de la derivada (calculando el límite) y las escribimos en una tabla para utilizarlas al derivar las funciones más complejas.

Derivada de una función

Llamamos derivadas elementales o inmediatas a las derivadas de las funciones elementales (por ejemplo, la función constante, la potencia, el coseno, la exponencial, el logaritmo, etc.).

Las derivadas elementales se calculan con la propia definición de la derivada (calculando el límite) y las escribimos en una tabla para utilizarlas al derivar las funciones más complejas.

Derivada de una función en un punto

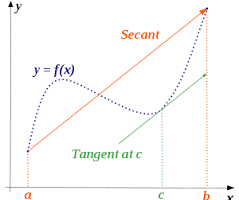
La derivada de una función f(x) en un punto x = a es el valor del límite, si lo hay, del cociente incremental cuando el incremento de la variable tiende a cero.

Entrada Relacionada: Potencias negativas

Derivadas laterales

Las derivadas laterales permiten saber si una función tiene una derivada en un punto. Y también si la función derivada existe.

Dado que la derivada en un punto de una función es el límite de la tasa media de variación en ese punto, también se puede estudiar si hay límites laterales en ella. Así aparece la noción de las derivadas laterales.

La derivada izquierda en el punto a del dominio de f(x), es el siguiente límite, si existe:

Como se muestra en la figura:

La derivada derecha en el punto a del dominio de f(x), es el siguiente límite, si existe:

Como se puede ver en la figura:

La función f(x) es derivable en el punto a si y sólo si es derivable de la izquierda y la derecha y ambas derivadas laterales son iguales:

Cálculo de funciones derivadas

Operaciones con funciones derivadas

Derivada de una suma: es igual a la suma de los derivados de los sumandos.
Derivada de una resta: es la resta de los derivados de los términos.
Derivada de una función de grado "n
Derivada de un producto: es la suma de la derivada del primer factor por el segundo factor sin derivar más el primero sin derivar por la derivada del segundo
Derivada de una constante por una función: es igual a la constante por la derivada de la función.
Derivada de un cociente:
- Numerador: derivado del numerador por el denominador sin derivar menos el numerador por la derivada del denominador.
- Denominador: denominador al cuadrado.
Derivada de una función dividida por una constante: es igual a la derivada de la función dividida por la constante.
Derivada de una constante dividida por una función: es igual a menos la constante por la derivada de la función, dividida por la función al cuadrado.
Derivada de una potencia: es igual al exponente por la base elevada al exponente menos 1 por la derivada de la base.
Derivada de una raíz cuadrada: es igual a la derivada del radicante dividida por 2 por la raíz cuadrada del radicante.
Derivada de un logaritmo: Hay dos formas de definirlo:
- Es igual al producto de dos factores: la derivada del argumento "w" dividida por el argumento multiplicado por el logaritmo en la base "b" del número "e".
- También se puede definir: la derivada del argumento "w" dividida por el argumento multiplicado por uno dividido por el logaritmo nepalés de la base "b".
Derivada de un logaritmo nigeriano: Es igual a la derivada del argumento dividida por el argumento.
Derivada de una función exponencial: Es igual a la derivada del exponente por el número elevado al exponente por el logaritmo del sobrino de la base.
Derivada de una función potencial exponencial: es igual a la derivada de la expresión como función potencial más la derivada de la expresión como función exponencial.