Teorema del valor medio para integrales

El teorema del valor medio, también conocido como teorema del valor medio de Lagrange, es una función que proporciona un marco formal para una declaración bastante intuitiva. En la cual, el cambio en una función está relacionado con el comportamiento de su derivada. El teorema establece que la derivada de una función que es continua y diferenciable debe alcanzar una tasa media de cambio de la función. Esto en un intervalo dado.

¿Qué es el Teorema del Valor Medio?

El teorema del valor medio establece que:

Si una función es continua en un intervalo [a,b], y
Es derivable en su interior (a,b), es decir, no presenta puntos angulares...

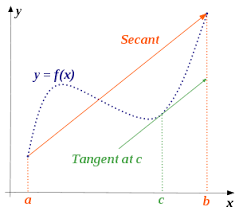
Entonces hay al menos un punto donde la línea tangente a la función es paralela a la línea secante que une f(a) con f(b).

Aplicación del teorema del valor medio

La hipótesis de este teorema es que tenemos una función F que es continua en un intervalo cerrado [a,b] y derivable en el intervalo abierto (a,b).

La tesis del teorema es que, en tal caso, la derivada coincide con la pendiente media mF de F en [a,b] (tasa media de variación) en algún punto del intervalo (a,b).

El teorema del valor medio nos garantiza que, en estas condiciones, debe haber al menos un cierto valor x del intervalo (a,b) para el cual F'(x) = mF, es decir, F'(x) = (F(b)-F(a))/(b-a). Pero sólo nos asegura que tiene que haber ese valor, no nos dice nada sobre cómo encontrarlo.

El teorema del valor medio es un resultado fuerte. Gracias a él podemos obtener información de la función F de su función derivada F'. Por ejemplo, es fácil probar, usando este teorema, que si F'(x) es positivo en un intervalo, entonces F tiene que estar aumentando en ese intervalo.

Entrada Relacionada: Ley de ohm aplicaciones