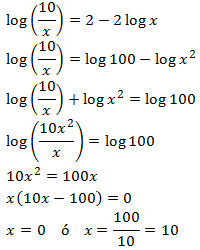
Ecuaciones logarítmicas
Las ecuaciones logarítmicas son aquellas en las que al menos una de las incógnitas es un logaritmo. Podemos expresarlo de una manera general como esta:
Estando en la base del logaritmo, x cualquier potencia e y el resultado de ese logaritmo.
Para poder resolver estas ecuaciones debemos recordar las propiedades de los logaritmos (suma, resta, división, multiplicación, etc.)
Cómo resolver ecuaciones logarítmicas
Una ecuación logarítmica es una ecuación cuya incógnita (o desconocida) se encuentra multiplicando o dividiendo los logaritmos, en sus bases o en el argumento de los logaritmos (dentro de los logaritmos).
Ejemplos de ecuaciones logarítmicas:
- Incógnita en el argumento:
La solución es x = 2.
- Incógnita en la base:
La solución es x = raíz cúbica de 7. - Incógnita multiplicando al logaritmo:
La solución es x = 5/log(3).
Pasos para resolver las ecuaciones logarítmicas
- Teniendo un solo logaritmo en ambos miembros de la ecuación
- Aplicamos las propiedades de los logaritmos:
- El producto de un número por un logaritmo se convierte en el logaritmo de una potencia.
- La suma de los logaritmos se convierte en el logaritmo de un producto.
- La diferencia de logaritmos se convierte en el logaritmo de un cociente.
Con esto obtenemos un solo logaritmo en ambos miembros de la ecuación log A = log B
- Resuelve la ecuación restante
Para obtener las posibles soluciones de la ecuación logarítmica resolvemos una ecuación que no es logarítmica. Puede ser una ecuación de primer grado, una ecuación de segundo grado u otro tipo.
Las soluciones que obtenemos son para esa ecuación y pueden no ser para la ecuación logarítmica, por lo que siempre debemos comprobar las soluciones.
- Comprobar la validez de las soluciones obtenidas.
Para comprobar las soluciones sustituimos los valores obtenidos de x en la ecuación logarítmica. Si la ecuación logarítmica se cumple y tiene sentido, ese valor de x será una solución, de lo contrario no.
Contenido