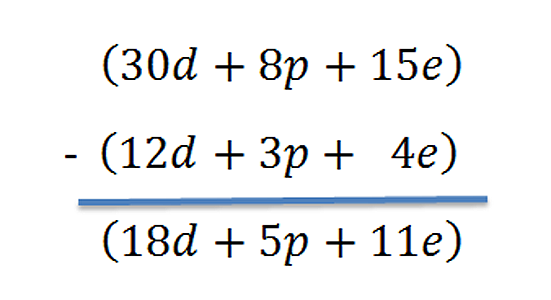
Resta de polinomios

Un polinomio es una expresión algebraica formada por la unión de dos o más constantes y variables, relacionadas mediante operaciones de sustracción, suma o multiplicación. Con los polinomios se pueden realizar diferentes cálculos como la resta.

Resta de polinomios

Para realizar una sustracción polinómica, es necesario agrupar los monomios (las expresiones de un solo término) según sus características y proceder a simplificar los que son similares. La operación propiamente dicha se realiza añadiendo al minuendo lo contrario de la sustracción.

Cómo restar polinomios

Para realizar la sustracción de dos o más polinomios, debemos primero identificar sus términos similares (mismo grado); agrupados estos términos, añadimos los coeficientes del primer polinomio con el opuesto del segundo polinomio. En algunos casos, si el polinomio no está completo, lo completamos con coeficientes iguales a cero (0). El resultado que obtenemos de restar dos o más polinomios es un solo polinomio.

Para restar binomios, trinomios, cuadrinomios o cualquier tipo de polinomio el procedimiento es el mismo; sólo se selecciona el método de preferencia y se procede a realizar la sustracción.

Existen dos métodos para resolver las sustracciones de polinomios; ambos son muy similares, pero aún así, no todos utilizan el mismo método a la hora de resolver las sustracciones:

Horizontalmente.
Verticalmente.

Propiedades de la sustracción de polinomios

Propiedad asociativa: Ser dos polinomios A(x) y B(x) se cumple:

(A(x) - B(x)) - C(x) = (A(x) - C(x)) - B(x)

Elemento neutro: Sea un polinomio P(x) y 0 un polinomio nulo cuyo valor numérico es cero, se cumple que:

P(x) - 0= P(x)

Elemento opuesto: Siendo A(x) un polinomio y -A(x) su opuesto (es decir, el mismo polinomio pero cambiado el + por - y el - por + de todos sus coeficientes) se cumple que

Entrada Relacionada: Cómo hacer fracciones

A(x) - A(x) = 0