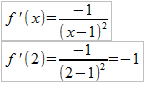Recta tangente a una curva en un punto
La línea tangente a una curva es la que coincide con la curva en un punto y con la misma derivada, es decir, el mismo grado de variación.
El conocimiento de la recta tangente nos permitirá resolver problemas sencillos: en primer lugar, podremos encontrar tangentes a cualquier función que pueda ser derivada, en cualquier punto, como se muestra en el primer ejemplo resuelto a continuación. En segundo lugar, y como se puede ver en el segundo ejemplo, se puede utilizar como condición en problemas más complejos.
Recta tangente
La línea tangente en el punto de un círculo es aquella línea que intercepta el círculo en un solo punto, pero la verdad es que tal definición no es suficiente para una curva en general porque en otros casos la línea tangente puede interceptar la curva en uno o más puntos, además de estar inclinada, horizontal o vertical.
Para obtener una definición adecuada de la recta tangente a la gráfica de una función en un punto, se utiliza el concepto de límite.
Recta normal
Si dibujas una perpendicular a la línea tangencial, obtienes la línea normal. Los gráficos muestran la línea tangente y la línea normal a la curva en un punto determinado.
Ejemplo de Recta tangente y recta normal a una curva en un punto
Encuentra la ecuación de la recta tangente en un punto.
A partir de la función f(x) y dado un punto a donde tenemos que calcular la línea tangente. Simplemente tenemos que calcular los datos que necesitamos sustituir en la fórmula.
1) Calcula cuánto es la función en el punto a, es decir, f(a)
2) Calcula la pendiente. Para ello calcularemos la derivada y sustituiremos el valor de x por el punto, es decir m=f '(a).
3) Sustituir en la fórmula de la ecuación de la recta tangente.
Contenido