Raíces de un polinomio
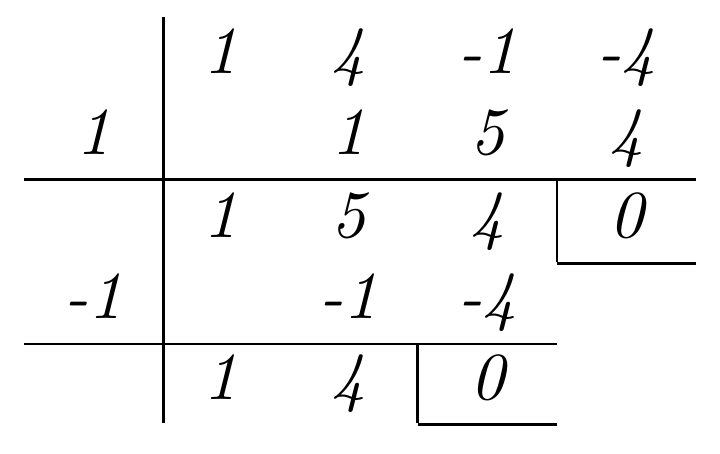
Las raíces de un polinomio son aquellos números que sustituyendo la variable (x) cancelan el polinomio. Las raíces de los polinomios que aparecen en estos ejercicios son enteros, así que puedes usar el método de Ruffini para encontrarlos.
Teorema del resto y teorema del factor
Por la aplicación de la regla de Ruffini para el cociente entre polinomios (ver t31), se sabe que al dividir un polinomio P (x) por un binomio x - m se obtiene un nuevo polinomio Q (x) de un grado inferior a P (x) y un resto de grado estrictamente inferior a 1, es decir, igual a una cantidad numérica r. Por lo tanto:
P (x) = Q (x) (x - m) + r
El valor numérico del polinomio P (x) que sustituye a x por m será P (m) = r. Este principio se conoce como teorema del resto, y afirma que el resto del cociente de un polinomio por un binomio x - m es igual al valor numérico que toma este polinomio por x = m.
De él se deduce como corolario el llamado teorema del factor, por el que se afirma que un polinomio P (x) es divisible por un binomio x - m si, y sólo si, el valor numérico de este polinomio para x = m es cero.
Se deduce como corolario el llamado teorema del factor, por el cual se afirma que un polinomio P (x) es divisible por un binomio x - m si, y sólo si, el valor numérico de este polinomio para x = m es cero.
Se dice que un número a es la raíz de un polinomio P(x), si P(a) = 0.
Así, si a es una raíz entera de un polinomio P(x) con coeficientes enteros, este valor a debe ser un divisor del término independiente de P(x).
Factorización del polinomio
A veces es práctico descomponer un polinomio complejo en el producto de otros más simples. Este procedimiento, llamado factorización, se basa en la aplicación de los teoremas del resto y del factor, y aplica la regla de Ruffini como técnica.
Para factorizar un polinomio, se actúa de la siguiente manera:
Se elabora una lista con todos los divisores del término independiente (que son candidatos a las raíces del polinomio).
Se determina cuáles de estos divisores son raíces del polinomio aplicando la regla de Ruffini a cada uno de ellos y seleccionando aquellos cuyo resto es cero.
Se toma el polinomio resultante de dividir el original por el binomio con la primera raíz, y se repiten los dos pasos anteriores.
Cuando se llega a una situación en la que ninguno de los divisores es la raíz (real) del polinomio, se considera que es irreducible.
Contenido