Potencia de un punto

Conjunto de todos los puntos del plano situados a la misma distancia de un punto fijo de ese plano, donde el punto fijo del plano se llama el centro del círculo y la distancia entre el centro y los puntos del círculo se llama el radio del círculo

Potencia de un punto

En la geometría elemental, la potencia de expresión de un punto se refiere a un resultado que relaciona las longitudes de los segmentos de línea que pasan por ese punto y que se cortan en un círculo fijo.

El término potencia para referirse a este concepto geométrico fue introducido por Jakob Steiner en el artículo de 1826 titulado Einige geometrische Betrachtungen ("Algunas observaciones geométricas") aunque el teorema al que se refiere ya se encuentra en los Elementos de Euclides

La potencia de un punto con respecto a un círculo es el producto de los segmentos de cualquier secante que pase por el punto, entre el punto y las intersecciones de la secante con el círculo.

Si P es un punto en el plano del círculo del centro en O y PA es cualquier secante que pase por P(fig 1), la potencia p de este punto será: p = PA . PB Si el punto está dentro del círculo, con Q, su potencia p' será: p'= QC . QD Si el punto está dentro del círculo, uno de los segmentos secantes es nulo y su potencia será por lo tanto cero.

Obsérvese que cuando el punto está fuera, como P los segmentos secantes están en el mismo lado de P sobre PA; mientras que si el punto está dentro, como Q, los segmentos están en un lado diferente del punto: se dice entonces que en el primer caso tienen la misma dirección y en el segundo caso dirección opuesta, la potencia cuando el punto está fuera se llama Positiva y negativa cuando está dentro.

Entrada Relacionada: Ecuaciones vectoriales

Cálculo de la Potencia

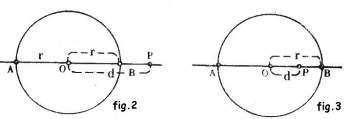
Como el valor de la potencia de un punto es independiente de la dirección de la secante que lo atraviesa, consideremos la secante que pasa por el centro de la circunferencia y analicemos los casos: Primer caso: El punto está fuera de la circunferencia. Sea P el punto, d su distancia al centro y r el radio de la circunferencia. fig 2

Tenemos : p = PA . PB = (d + r ) (d – r ) = d² – r²

2do Caso: El punto es interior de la circunferencia (Fig 3): Si P es el punto p = PA . PB = (r + d ) (r –d ) = r² – d² Notese que por ser r² – d² = - (d² – r² ), tomando como valor de la potencia en los dos casos la diferencia d² – r² en el segundo caso es negativa como de había convenido

3er caso: El punto esta en la circunferencia: En este caso, como d = r resulta p= 0

Contenido