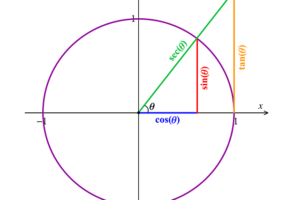
Teorema de Pitágoras El teorema de Pitágoras relaciona la longitud de las piernas y la hipotenusa. Establece que: Todos los triángulos rectos cumplen que el cuadrado de la hipotenusa es igual a la suma de los lados adyacentes al ángulo recto (patas) al cuadrado. Es decir: Teorema de la altura…

Inecuaciones racionales Los signos de desigualdad que se utilizan en las inecuaciones son: <, >, ≤ y ≥: a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3. a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 > 2. a ≤ b significa "a es menor o igual que b". Por ejemplo: 2 ≤ 2. a ≥ b significa "a es mayor o igual que b". Por…

Distribuciones muestrales ejercicios resueltos El jefe de la sede de una empresa afirma que las edades de sus empleados siguen una distribución normal con una media de 41 años y una desviación estándar de 5 años. Por otro lado, el jefe de una sucursal de esa empresa en otro país,…

¿Qué son las ecuaciones matriciales? Las ecuaciones matriciales son como las ecuaciones normales, pero en lugar de estar formadas por números, están formadas por matrices. Por ejemplo: Por lo tanto, la solución X también será una matriz. Como saben, las matrices no pueden ser divididas. Por lo tanto, NO PUEDES…

Racionalización de radicales La racionalización se utilizó para dejar los resultados más simplificados. Dejando sólo los radicales en el numerador, se obtiene que, cuando se desea hacer una aproximación más exacta del resultado de la división, ésta no tiene que volver a empezar y se puede seguir dividiendo a partir…

Notación científica convertidor Cualquier número puede ser representado con notación científica, expresándolo como el producto de un número (con o sin decimales) entre -10 y 10 y una potencia de 10. Ejemplos: Año luz = 9,46⋅1012km Diámetro atómico = 2,5⋅10−10m Para simplificar, es posible eliminar el 10 de la potencia y sustituirlo…

Intervalos de una función Función creciente A medida que el valor de x aumenta, el valor de y aumenta. La definición es la siguiente: una función se incrementa en un intervalo si cumple con eso: Veamos un ejemplo gráfico: Función decreciente A medida que el valor de x aumenta, el…

Funciones trigonométricas Función trigonométrica: conjunto de pares ordenados (x;y), de modo que el valor de "x" es la medida del ángulo en radianes, y la componente "y" es la relación trigonométrica de "x". Dominio: el dominio de una función trigonométrica es el conjunto de valores que toma la variable "x".…

Coeficiente de correlación de pearson Para llevar a cabo la correlación de Pearson, debe cumplirse lo siguiente: La escala de medición debe ser una escala de intervalo o de proporción. Las variables deben estar distribuidas de manera aproximada. La asociación debe ser lineal. No debe haber valores atípicos en los…

Propiedades de los triángulos La suma de los ángulos interiores de un triángulo es siempre de 180º. Un triángulo no puede tener más de un ángulo recto u obtuso. Cualquier lado de un triángulo es siempre menor que la suma de los otros dos lados, pero mayor que su diferencia.…