Método de reducción
El último de los métodos analíticos que aprenderemos a utilizar en esta Unidad para resolver sistemas lineales de dos ecuaciones con dos incógnitas es el método de reducción. En resumen, consiste en multiplicar una o ambas ecuaciones por algún número(s) para obtener un sistema equivalente al inicial en el que los coeficientes de x o y son iguales pero de signo opuesto. Luego se suman las ecuaciones del sistema para obtener una única ecuación de primer grado con una desconocida. Una vez resuelta, hay dos opciones para encontrar la otra desconocida: una es aplicar de nuevo el mismo método (sería la opción más pura de reducción), la otra es sustituir la desconocida encontrada en una de las ecuaciones del sistema y borrar la otra.
Método de reducción ejercicios resueltos paso por paso
Las ecuaciones se multiplican por los números correspondientes de manera que, en una de las incógnitas, los coeficientes son iguales pero de signo opuesto,
- Se suman las dos ecuaciones del nuevo sistema, equivalentes a la anterior.
- La ecuación lineal de una incógnita resultante se resuelve.
- Para este paso hay dos opciones:
- El proceso se repite con el otro desconocido.
- Reemplaza la incógnita ya encontrada en una de las ecuaciones del sistema y resuelve la otra.
De nuevo queda claro que todas las aclaraciones hechas en la sección del método de sustitución sobre la discusión del sistema para saber si tiene solución o no y cuántas (si las tiene), son igualmente válidas en este método.
Ejemplo de método de reducción
Los pasos a seguir son los siguientes:
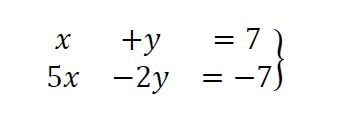
Primero, tenemos que preparar las dos ecuaciones, si es necesario, multiplicándolas por los números apropiados.
En este caso, queremos reducir la "y" de nuestro sistema, por lo que multiplicamos la primera ecuación por 2.
2(x+y=7)
5x-2y=-7
Así, el sistema se queda:

Si nos fijamos, sumando las ecuaciones la y nos desaparece.

Y nos quedaría:
7x=7
x=7/7=1
x=1
Finalmente, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.
y= 7-x
y=7-1=6
y=6
La solución de nuestro sistema es x=1 e y =6.
Contenido