Matriz inversa por gauss jordan
Invertir la matriz. Se dice de la Matriz cuadrada A-1 del orden N que dada, A una matriz cuadrada no singular del mismo orden, satisface AA-1=A-1A=IN..
Matriz inversa
Dada la matriz cuadrada A de orden N se dice que es una matriz invertible si y sólo si el determinante de A no es nulo.
Si A es una matriz invertible, la matriz cuadrada A-1 de orden N es la matriz inversa de A tal que AA-1=A-1A=IN.
Propiedades de la Matriz inversa
- En relación con la inversión:
- Una matriz cuadrada A es invertible si hay otra matriz cuadrada B tal que AB=BA=I.
- Una matriz es invertible:
- Es cuadrada.
- No es singular.
- Si una matriz A de orden n es invertible, entonces su rango también es n.
- La matriz inversa, si existe, es única.
- (AB)-1=A-1B-1
- (AT)-1=(A-1)T
- (A-1)-1=A
- I-1=I
Matriz inversa por gauss jordan
Consideremos una matriz 3x3 arbitraria:

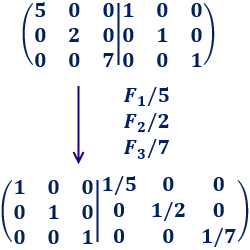
La ampliamos con la matriz identidad de orden 3.

Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: ![]() .
.
![]()

![]()

![]()

![]()

![]()

La matriz inversa es:

Contenido