Imagen de una función

El dominio de una función es el conjunto de valores de la variable independiente, o el valor x, para el que se define la función. La imagen de una función son los valores de la variable dependiente, o el valor y, sobre el dominio. Para simplificar, el dominio de una función es todos los valores de x que tienen su valor en y. Y la imagen es todos los valores reales de y que resultan de todos los valores del dominio.

¿Qué es la imagen de una función?

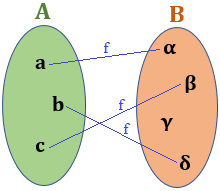
Una función es una correspondencia entre dos conjuntos no vacíos A y B, en la que por cada elemento que pertenece al conjunto A sólo hay un elemento, y sólo uno, que pertenece al conjunto B al que está asociado o corresponde.

Para simbolizar que se ha establecido una función f , de un conjunto A en un conjunto B, se utiliza la siguiente notación:

f : A → B

Criterios de función

En un sentido abstracto, el cálculo de una función consiste en examinar la correspondencia general de "y" con respecto a "x" , expresada en la fórmula abstracta:

y = f(x)

Esta fórmula establece que la magnitud "y" es, de manera general, una función de "x".

Obsérvese que la magnitud "y" corresponde a lo que llamaremos "imagen", y que depende del valor asignado a "x" (que será la "vista previa") en f(x).

La notación y = f (x) se lee "y" es una función de "x" o "y" es igual a f de x (esta notación no significa f por (x)). Obviamente, en lugar de "x" e "y" podríamos haber usado "variable", y escribirlo así

Variable dependiente = f (variable independiente)

Imagen de una función ejercicios resueltos

Ejemplo 1

Para determinar si un gráfico representa una función, se utiliza la prueba de la línea vertical, que consiste en lo siguiente:

Entrada Relacionada: Operaciones con porcentajes

Se dibuja una línea perpendicular al eje x y se mueve imaginativamente a la derecha y a la izquierda.

Si las líneas siempre cortan el gráfico en un solo punto, el gráfico corresponde a una función.

Si al menos una de las líneas corta el gráfico en dos o más puntos, el gráfico no corresponde a una función.

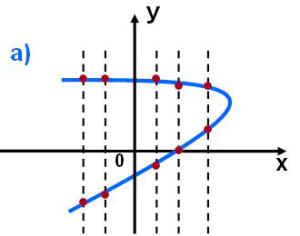
No corresponde a una función.

Como puedes ver, cuando dibujas una línea perpendicular al eje "x" y la mueves a los lados, varias de ellas cortan el gráfico en dos puntos. Sólo una de ellas es suficiente.

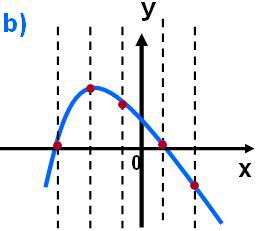
Corresponde a una función.

Como puedes ver, cuando dibujas una línea perpendicular al eje "x" y la mueves a los lados, siempre corta el gráfico en un punto.

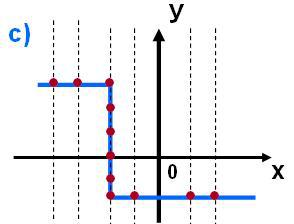
No corresponde a una función.

Como puedes ver, cuando dibujas una línea perpendicular al eje x y la mueves a los lados, varias de ellas cortan la gráfica en un punto. Sin embargo, una de ellas lo hace en varios puntos y con sólo una de ellas haciéndolo, es suficiente para que no sea una función.

Contenido