Eliminación de parámetros calculo vectorial

El cálculo vectorial se utiliza ampliamente para resolver sistemas de ecuaciones e incluso cualquier problema complejo de ingeniería puede convertirse en un sistema de ecuaciones, que a su vez puede resolverse mediante cálculos matriciales, que están relacionados con el cálculo vectorial. Especialmente en el ámbito de la ingeniería mecánica, cabe señalar que el cálculo vectorial se utiliza ampliamente en los problemas de dinámica y cinemática de los mecanismos, es decir, para estudiar los movimientos, velocidades y aceleraciones de los elementos que componen los diversos tipos de mecanismos.

Eliminación de parámetros calculo vectorial

Discute y resuelve el siguiente sistema de ecuaciones lineales dependiente de parámetros:

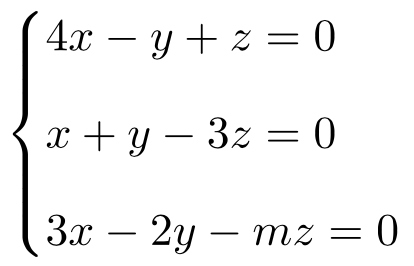
En primer lugar, hacemos es la matriz A y la matriz ampliada A’ del sistema:

Ahora tenemos que hallar el rango de la matriz A. Para ello, miramos si el determinante de toda la matriz es diferente de 0:

El resultado del determinante de A depende del valor de m. Para ello, igualamos el resultado obtenido a 0 y resolvemos la ecuación:

Por lo tanto, cuando m vale -4, el determinante de A será 0. Y cuando m es diferente de -4 el determinante de A será diferente de 0:

m≠-4:

Como acabamos de ver, cuando m es diferente de -4, el determinante de A es diferente de 0.

Además, el rango de la matriz A' también es 3, porque dentro de ella hay una submatriz de 3×3 cuyo determinante es diferente de 0. Y no puede ser de rango 4 ya que no podemos hacer ningún determinante de 4×4.

Por lo tanto, aplicando el teorema de Rouché-Frobenius sabemos que es un Sistema Compatible Determinado (SCD), porque el rango de A es igual al rango de A' y el número de incógnitas.

Entrada Relacionada: Common denominator

Una vez que sabemos que el sistema es un SCD, aplicamos la regla de Cramer para resolverlo. Para ello, recuerda que la matriz A, su determinante y la matriz A'.

El rango de la matriz A es igual al rango de la matriz A' pero estos dos son menores que el número de incógnitas del sistema (3), por lo tanto, según el teorema de Rouché-Frobenius es un Sistema Compatible Indeterminado (SCI):

Es un sistema SCI, así que tenemos que transformar el sistema para resolverlo.

Finalmente, una vez que hemos transformado el sistema, aplicamos la regla de Cramer. Para hacer esto, primero resolvemos el determinante de A.

Para calcular x con la regla de Cramer, cambiamos la primera columna del determinante de A por la columna de términos independientes y la dividimos por el determinante de A:

Para calcular lo desconocido y con la regla de Cramer, cambiamos la segunda columna del determinante de A a la columna de términos independientes y la dividimos por el determinante de A: